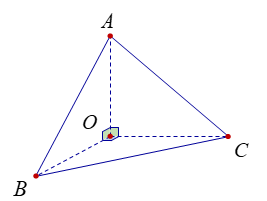
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy ABC là tam giác đều cạnh a. Góc giữa \(CA'\) và mặt \((AA'B'B)\) bằng \(30{}^\circ \). Gọi d(AI’,AC) là khoảng cách giữa \(A'I\) và AC, kết quả tính d(AI’,AC) theo a với I là trung điểm AB là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Ta có : \(\left\{ \begin{array}{l} CI \bot AB\\ CI \bot AA'\,\,(AA' \bot (ABC))\\ Trong\,\,(AA'B'B):\,\,AB \cap AA' = \left\{ A \right\} \end{array} \right. \Rightarrow CI \bot (AA'B'B)\)
Suy ra góc giữa CA’ và \((AA'B'B)\) chính là góc
giữa CA’ và IA’ và bằng góc \(\widehat{CA'I}=30{}^\circ \)
Do đó \(A'I=\frac{IC}{\tan \widehat{CA'I}}=\frac{3a}{2}\) ; với \(IC=\frac{AB\sqrt{3}}{2}=\frac{a\sqrt{3}}{2}\)
Suy ra: \(AA'=\sqrt{A'{{I}^{2}}-A{{I}^{2}}}=\sqrt{\frac{9{{a}^{2}}}{4}-\frac{{{a}^{2}}}{4}}=a\sqrt{2}\)
Kẻ \(Ix\parallel AC\). Khi đó \(d(AC,A'I)=d(AC,(A'I,Ix))=d(A,(A'I,Ix))\)
Kẻ \(AE\bot Ix\) tại E và \(AF\bot A'E\) tại F. Ta chứng minh được: \(d\left( A,(A'I,Ix) \right)=AF\)
Ta có: \(AE=AI.\sin \widehat{AIE}=\frac{a}{2}.\sin 60{}^\circ =\frac{a\sqrt{3}}{4}\) và \(\frac{1}{A{{F}^{2}}}=\frac{1}{A'{{A}^{2}}}+\frac{1}{A{{E}^{2}}}=\frac{1}{2{{a}^{2}}}+\frac{16}{3{{a}^{2}}}=\frac{35}{6{{a}^{2}}}\Rightarrow AF=\frac{a\sqrt{210}}{35}\)
Vậy: \(d\left( AC,A'I \right)=AF=\frac{a\sqrt{210}}{35}\).
Câu hỏi liên quan
-
Cho hình chóp S.ABC có đáy ABC là tam giác cân, AB = BC = 2a, \(\widehat{ABC}={{120}^{0}}\), SA = 3a và SA vuông góc với mặt phẳng đáy. Tính khoảng cách d từ điểm A đến mặt phẳng (SBC).
-
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu của S lên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABD. Mặt bên SAB tạo với đáy một góc 600. Tính theo a khoảng cách từ B đến mặt phẳng (SAD)?
-
Cho hình thang vuông ABCD vuông ở A và D, AD = 2a. Trên đường thẳng vuông góc tại D với (ABCD) lấy điểm S với \(SD = a\sqrt 2 \). Tính khỏang cách giữa đường thẳng DC và (SAB).
-
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A\), \(AB=a,\text{ }AC=a\sqrt{3}\). Tam giác \(SBC\) đều và nằm trong mặt phẳng vuông với đáy. Tính khoảng cách từ \(B\) đến mặt phẳng \(\left( SAC \right)\).
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính theo a khoảng cách từ điểm A đến mặt phẳng (A'BC)
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a. Cạnh bên \( SA = a\sqrt 2 \) và vuông góc với đáy (ABCD). Tính khoảng cách d từ điểm B đến mặt phẳng (SCD)
-
Cho hình chóp O.ABC có đường cao \(OH = \frac{{2a}}{{\sqrt 3 }}\). Gọi M và N lần lượt là trung điểm của OA và OB. Khoảng cách giữa đường thẳng MN và (ABC) bằng:
-
Cho hình chóp A.BCD có cạnh AC vuông góc (BCD) và BCD là tam giác đều cạnh bằng a. Biết \( AC = a\sqrt 2\) và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng
-
Cho hình chóp S.ABCD có \(SA \bot \left( {ABCD} \right)\), đáy ABCD là hình chữ nhật với \(AC = a\sqrt 5 \) và \(BC = a\sqrt 2 \). Tính khoảng cách giữa SD và BC.
-
Cho hình chóp S.ABCD có đáy là hình chữ nhật, \(AB=a,AD=2a\) ; cạnh bên \(SA=a\) và vuông góc với đáy. Khoảng cách từ điểm A tới mặt phẳng \(\left( SBD \right)\) là
-
Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a. Gọi M, N, P lần lượt là trung điểm của AD, DC, A'D'. Tính khoảng cách giữa hai mặt phẳng (MNP) và (ACC').
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với đáy và \(SA = a\sqrt 3 \). Biết diện tích tam giác SAB là \(\frac{{{a^2}\sqrt 3 }}{2}\). Khoảng cách từ điểm B đến \(\left( {SAC} \right)\) là:
-
Cho tứ diện đều ABCD có cạnh bằng a. Khoảng cách từ A đến (BCD) bằng bao nhiêu?
-
Cho hình chóp A.BCDcó cạnh AC vuông góc BCD và BCD là tam giác đều cạnh bằng a. Biết \(AC = a\sqrt 2\) , khoảng cách từ A đến đường thẳng BD bằng:
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right),SA = a\sqrt 5 \). Tính khoảng cách từ D đến mặt phẳng \(\left( {SAB} \right)\).
-
Bên cạnh con đường trước khi vào thành phố người ta xây một ngọn tháp đèn lộng lẫy. Ngọn tháp hình tứ giác đều S.ABCD cạnh bên SA = 600 mét, góc \( \widehat {SAB} = {15^0}\) . Do có sự cố đường dây điện tại điểm Q (là trung điểm của SA) bị hỏng, người ta tạo ra một con đường từ A đến Q gồm bốn đoạn thẳng: AM, MN, NP, PQ (hình vẽ). Để tiết kiệm kinh phí, kỹ sư đã nghiên cứu và có được chiều dài con đường từ A đến Q ngắn nhất. Tính tỉ số \( k = \frac{{AM + MN}}{{NP + PQ}}\)
-
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I với \(AB = 2a\sqrt 3 ;BC = 2a\). Biết chân đường cao H hạ từ đỉnh S xuống đáy ABCD trùng với trung điểm đoạn DI và SB hợp với mặt phẳng đáy (ABCD) một góc 60o. Khoảng cách từ D đến (SBC) tính theo a bằng
-
Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng \(a\sqrt 3 \). Gọi H là trọng tâm tam giác ABC, \({d_1}\) khoảng cách từ A đến mặt phẳng \(\left( {SBC} \right), {d_2}\) khoảng cách từ H đến mặt phẳng \(\left( {SBC} \right)\). Khi đó \({d_1} + {d_2}\) có giá trị bằng
-
Cho hình chóp SABC có \(SA \bot \left( {ABC} \right)\), tam giác ABC vuông tại B và có BC = a, Tính khoảng cách từ C đến mặt phẳng \(\left( {SAB} \right)\).
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Biết hình chóp S.ABC có thể tích bằng \({{a}^{3}}\). Tính khoảng cách d từ điểm A đến mặt phẳng (SBC).
