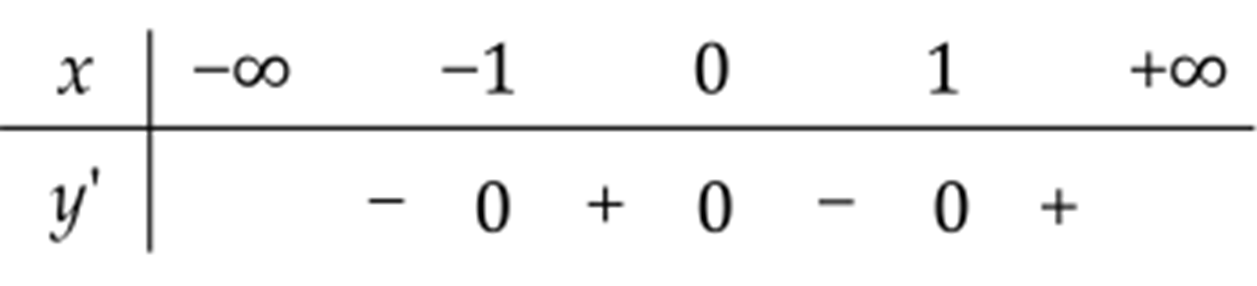Bộ Đề Kiểm Tra Giữa Học Kì I - Toán 12 - Cánh Diều - Đề 1
22 câu hỏi 60 phút
Gọi I là trung điểm của AB và điểm M bất kì khác I, A, B. Khẳng định nào sau đây sai?
\(\overrightarrow{IA}+\overrightarrow{IB}=\vec{0}\)
\(\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\)
IA = IB
\(\overrightarrow{IA}=\overrightarrow{IB}\)
I là trung điểm của AB nên
+ \(\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\);
+ \(IA=IB\) và hai vectơ \(\overrightarrow{IA};\overrightarrow{IB}\) ngược hướng.
Do đó \(\overrightarrow{IA}=-\overrightarrow{IB}\) hay \(\overrightarrow{IA}+\overrightarrow{IB}=\vec{0}\).
Danh sách câu hỏi:
I là trung điểm của AB nên
+ \(\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\);
+ \(IA=IB\) và hai vectơ \(\overrightarrow{IA};\overrightarrow{IB}\) ngược hướng.
Do đó \(\overrightarrow{IA}=-\overrightarrow{IB}\) hay \(\overrightarrow{IA}+\overrightarrow{IB}=\vec{0}\).
\(\overrightarrow{AB}=(3-1;(-5)-2;2-(-3))=(2;-7;5)\).
Ta có: \(\vec{a}=2\vec{i}+\vec{j}-2\vec{k}\Rightarrow \vec{a}=(2;1;-2)\Rightarrow |\vec{a}|=\sqrt{{{2}^{2}}+{{1}^{2}}+{{2}^{2}}}=3\).
Tập xác định: \(D=\mathbb{R}\backslash \{2\}\).
Lại có \({{y}^{\prime }}=-\frac{10}{{{(2x-4)}^{2}}}<0,\forall x\in D\)
nên hàm số luôn nghịch biến trên mỗi khoảng \((-\infty ;2)\) và \((2;+\infty )\).
Dựa vào bảng xét dấu của đạo hàm ta có trong khoảng \(\left( 0;+\infty \right)\) hàm số có duy nhất một điểm cực trị và điểm đó là điểm cực đại của hàm số.
Vậy trong khoảng \(\left( 0;+\infty \right)\) hàm số đạt giá trị lớn nhất tại \(x=1\) hay \(\underset{\left( 0;+\infty \right)}{\mathop{\max }}\,f(x)=f(1)\).
Câu 8:
Phương trình tiếp tuyến của đồ thị hàm số \(y=\frac{2x+1}{x-1}\) tại điểm có hoành độ \(x=2\) là
Câu 10:
Giá trị lớn nhất của hàm số \(y=-{{x}^{4}}+4{{x}^{2}}\) trên đoạn \(\left( -1;2 \right)\) bằng
Câu 13:
Cho hình lăng trụ tam giác \(ABC\cdot A'B'C'\).
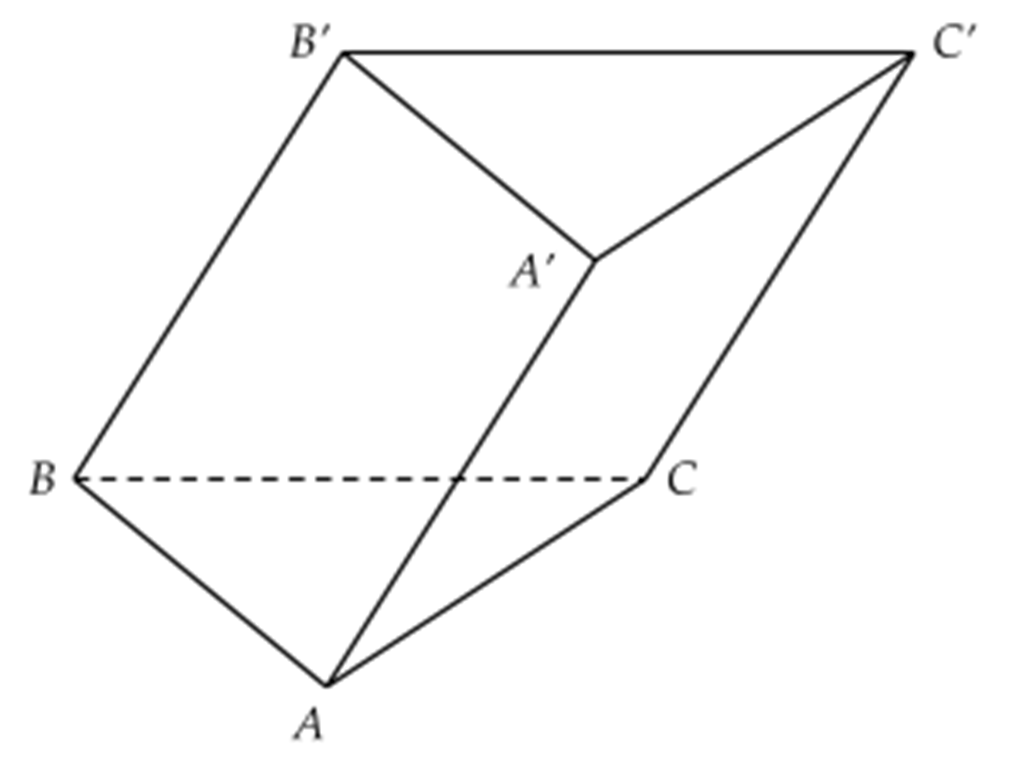
\(\overrightarrow{A{{A}^{\prime }}}+\overrightarrow{B{{B}^{\prime }}}=2\overrightarrow{C{{C}^{\prime }}}\)
\(\overrightarrow{AB}-\overrightarrow{C{{C}^{\prime }}}-\overrightarrow{{{A}^{\prime }}{{B}^{\prime }}}=\overrightarrow{B{{B}^{\prime }}}\)
\(\overrightarrow{B{{B}^{\prime }}}+2\overrightarrow{BC}+\overrightarrow{A{{A}^{\prime }}}=2\overrightarrow{B{{C}^{\prime }}}\)
\(\overrightarrow{A{{B}^{\prime }}}+\overrightarrow{BA}+2\overrightarrow{C{{C}^{\prime }}}=3\overrightarrow{B{{B}^{\prime }}}\)
Câu 14:
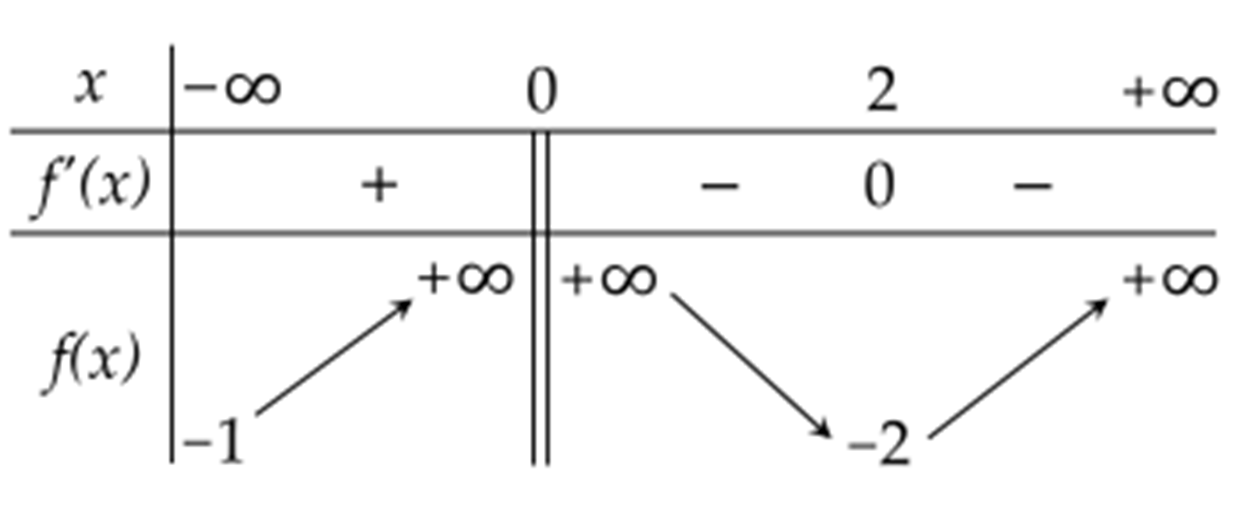
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
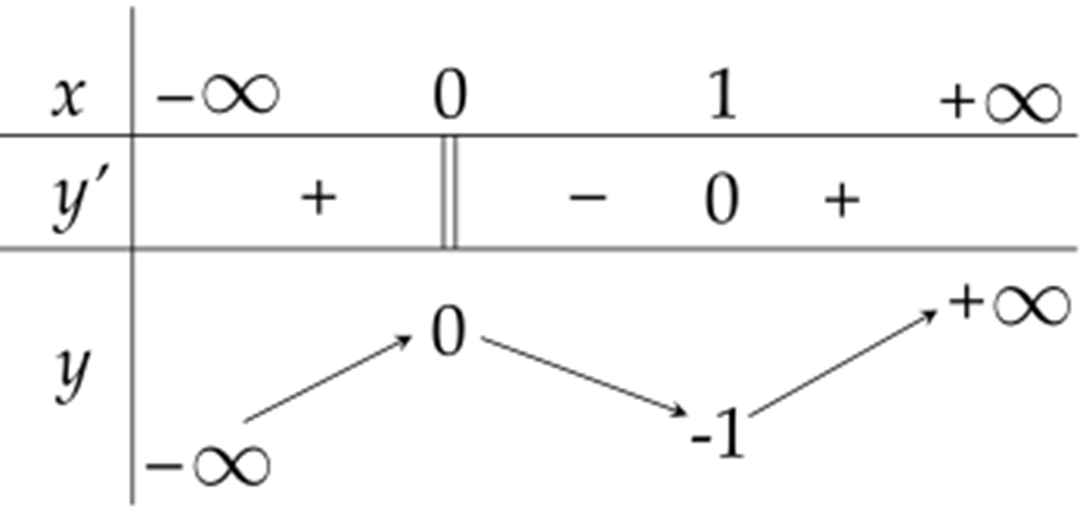
Hàm số \(y=f(x)\) có giá trị cực tiểu bằng 1
Đồ thị hàm số \(y=f(x)\) có điểm cực tiểu là \((1;-1)\)
Hàm số \(y=f(x)\) đạt cực đại tại \(x=0\)
Hàm số \(y=f(x)\) có đúng một cực trị
Câu 15:
Ông An muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng 288 288 \({{m}^{3}}\). Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500 000 đồng/\({{m}^{2}}\). Ba kích thước của bể được mô tả như hình vẽ dưới \((a(m)>0,c(m)>0)\).
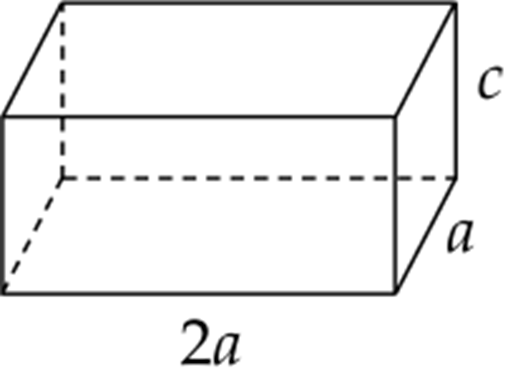
Nếu ông An biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất (Biết độ dày thành bể và đáy bể không đáng kể). Khi đó:
Diện tích các mặt cần xây là \(S=2{{a}^{2}}+6ac\)
\(2{{a}^{2}}c=280\)
Diện tích các mặt cần xây nhỏ nhất là \(216~{{\text{m}}^{2}}\)
Chi phí thấp nhất để xây dựng bể đó là 108 triệu đồng
Câu 16:
Cho hàm số \(y=f(x)=\sqrt{x-1}+\sqrt{9-x}\)
Tập xác định của hàm số \(y=f(x)\) là \(D=(1;9)\)
\({{f}^{\prime }}(5)=0\)
Hàm số \(y=f(x)\) đạt giá trị lớn nhất tại \(x=1\)
Tập giá trị của hàm số \(y=f(x)\) là \(T=(2\sqrt{2};4)\)