Câu hỏi:
Cho hàm số \(y=f(x)\) có đồ thị hàm số \(y=f'(x)\) như hình vẽ.
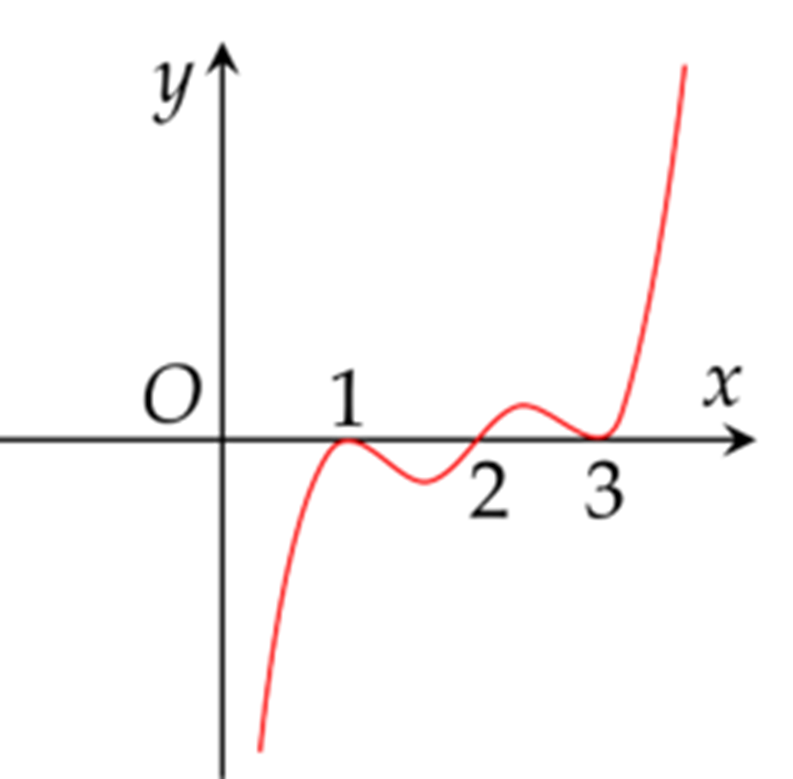
Số điểm cực trị của hàm số \(y=f(x)\) là
Đáp án đúng: D
Từ đồ thị hàm số \(y=f'(x)\) ta thấy \(f'(x)\) đổi dấu một lần qua điểm \(x=2\).
Do đó hàm số \(y=f(x)\) có 1 điểm cực trị.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Bộ Đề Kiểm Tra Giữa Học Kì I - Toán 12 - Cánh Diều là tài liệu học tập hữu ích giúp học sinh ôn tập và hệ thống lại kiến thức đã học. Với các dạng bài trắc nghiệm và tự luận phong phú, đề thi giúp học sinh rèn luyện khả năng tính toán, tư duy logic, đồng thời nâng cao kỹ năng giải quyết vấn đề một cách hiệu quả. Đây là công cụ hỗ trợ đắc lực để chuẩn bị cho các kỳ thi quan trọng.
Câu hỏi liên quan
Cho hình lăng trụ tam giác \(ABC\cdot A'B'C'\).
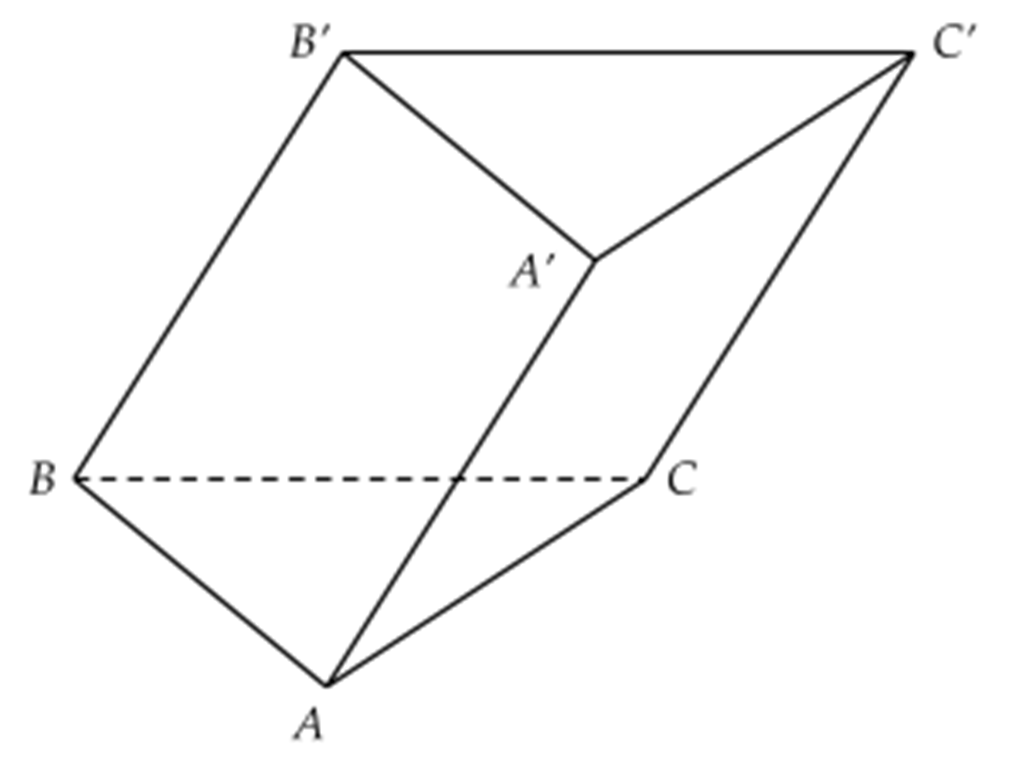
\(\overrightarrow{A{{A}^{\prime }}}+\overrightarrow{B{{B}^{\prime }}}=2\overrightarrow{C{{C}^{\prime }}}\)
\(\overrightarrow{AB}-\overrightarrow{C{{C}^{\prime }}}-\overrightarrow{{{A}^{\prime }}{{B}^{\prime }}}=\overrightarrow{B{{B}^{\prime }}}\)
\(\overrightarrow{B{{B}^{\prime }}}+2\overrightarrow{BC}+\overrightarrow{A{{A}^{\prime }}}=2\overrightarrow{B{{C}^{\prime }}}\)
\(\overrightarrow{A{{B}^{\prime }}}+\overrightarrow{BA}+2\overrightarrow{C{{C}^{\prime }}}=3\overrightarrow{B{{B}^{\prime }}}\)
Phương án 1:
Ta có \(\overrightarrow{A{{A}^{\prime }}}=\overrightarrow{B{{B}^{\prime }}}=\overrightarrow{C{{C}^{\prime }}}\).
Suy ra \(\overrightarrow{A{{A}^{\prime }}}+\overrightarrow{B{{B}^{\prime }}}=\overrightarrow{C{{C}^{\prime }}}+\overrightarrow{C{{C}^{\prime }}}=2\overrightarrow{C{{C}^{\prime }}}\).
Phương án 2:
\(\begin{array}{*{35}{l}} \overrightarrow{AB}-\overrightarrow{C{{C}^{\prime }}}-\overrightarrow{{{A}^{\prime }}{{B}^{\prime }}} \\ =\overrightarrow{AB}-\overrightarrow{A{{A}^{\prime }}}-\overrightarrow{{{A}^{\prime }}{{B}^{\prime }}} \\ =\overrightarrow{{{A}^{\prime }}B}-\overrightarrow{{{A}^{\prime }}{{B}^{\prime }}} \\ =\overrightarrow{{{B}^{\prime }}B}\ne \overrightarrow{B{{B}^{\prime }}}. \\ \end{array}\)
Phương án 3:
\(\begin{array}{*{35}{l}} \overrightarrow{B{{B}^{\prime }}}+2\overrightarrow{BC}+\overrightarrow{A{{A}^{\prime }}} \\ =2\overrightarrow{B{{B}^{\prime }}}+2\overrightarrow{BC} \\ =2\overrightarrow{B{{C}^{\prime }}}. \\ \end{array}\)
Phương án 4:
Ta có:
\(\begin{array}{*{35}{l}}\overrightarrow{A{{B}^{\prime }}}+\overrightarrow{BA}+2\overrightarrow{C{{C}^{\prime }}} \\ =\overrightarrow{A{{B}^{\prime }}}+\overrightarrow{{{B}^{\prime }}{{A}^{\prime }}}+2\overrightarrow{C{{C}^{\prime }}} \\ =\overrightarrow{A{{A}^{\prime }}}+2\overrightarrow{C{{C}^{\prime }}} \\ =\overrightarrow{B{{B}^{\prime }}}+2\overrightarrow{B{{B}^{\prime }}} \\ =3\overrightarrow{B{{B}^{\prime }}}. \\ \end{array}\)
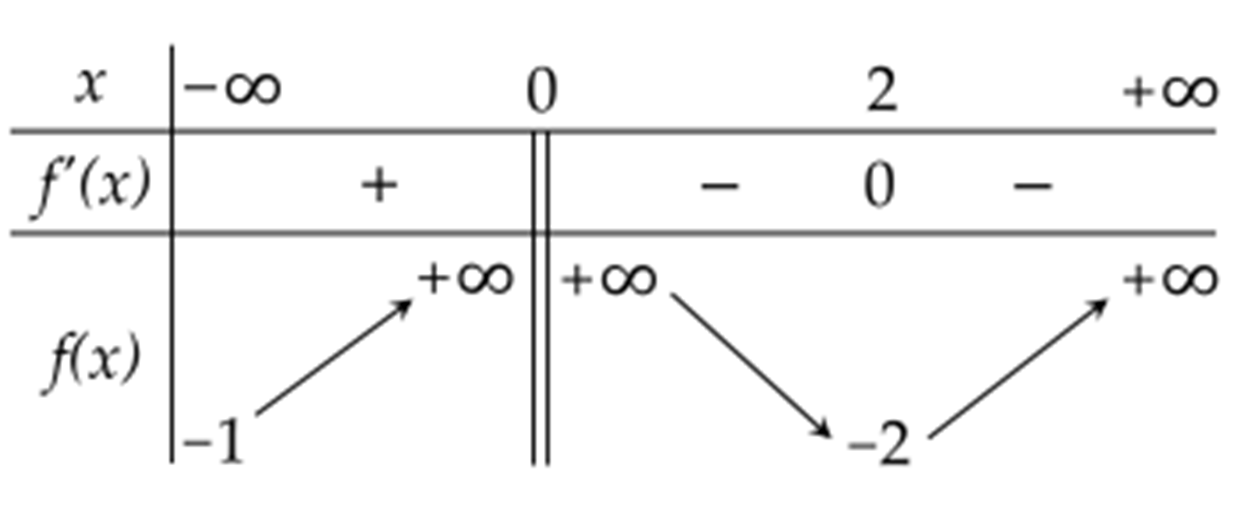
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
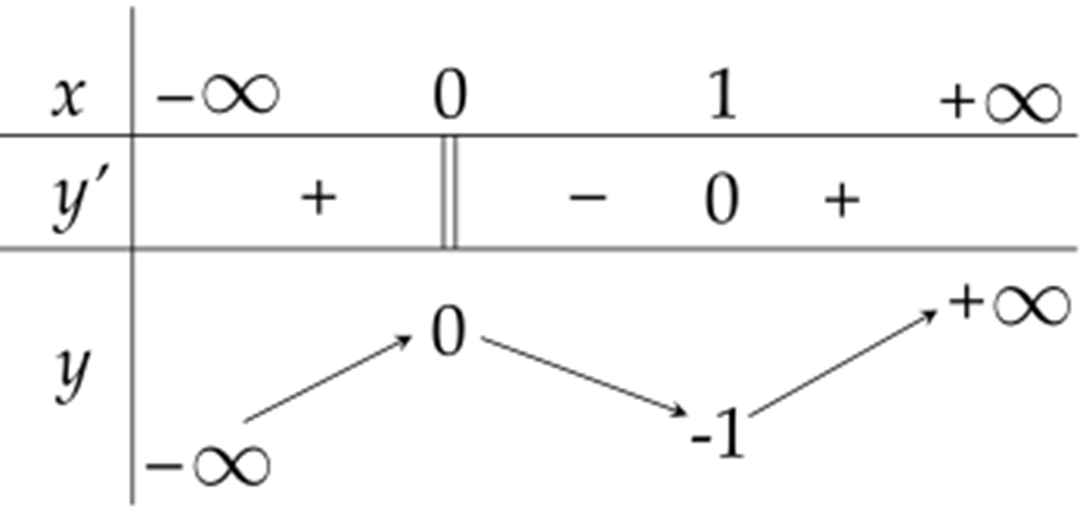
Hàm số \(y=f(x)\) có giá trị cực tiểu bằng 1
Đồ thị hàm số \(y=f(x)\) có điểm cực tiểu là \((1;-1)\)
Hàm số \(y=f(x)\) đạt cực đại tại \(x=0\)
Hàm số \(y=f(x)\) có đúng một cực trị
Dựa vào bảng biến thiên ta thấy:
+ Hàm số \(y=f(x)\) đạt cực đại tại \(x=0\) và đạt cực tiểu tại \(x=1\).
+ Giá trị cực tiểu của hàm số bằng \(-1\).
+ Đồ thị hàm số \(y=f(x)\) có điểm cực tiểu là \((1;-1)\).
Ông An muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng 288 288 \({{m}^{3}}\). Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500 000 đồng/\({{m}^{2}}\). Ba kích thước của bể được mô tả như hình vẽ dưới \((a(m)>0,c(m)>0)\).
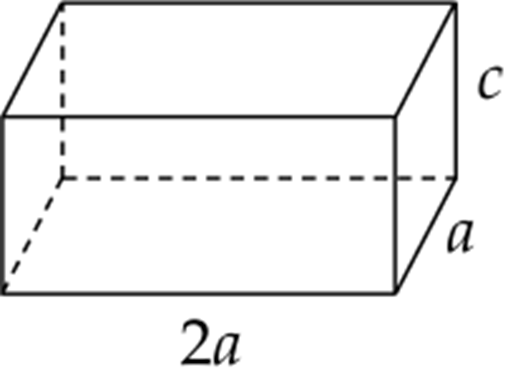
Nếu ông An biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất (Biết độ dày thành bể và đáy bể không đáng kể). Khi đó:
Diện tích các mặt cần xây là \(S=2{{a}^{2}}+6ac\)
\(2{{a}^{2}}c=280\)
Diện tích các mặt cần xây nhỏ nhất là \(216~{{\text{m}}^{2}}\)
Chi phí thấp nhất để xây dựng bể đó là 108 triệu đồng
a) Từ hình vẽ ta có ba kích thước của bể là \(a,2\text{ }a,c\).
Ta có diện tích cách mặt cần xây là \(S=2{{a}^{2}}+4ac+2ac=2{{a}^{2}}+6ac\).
b) Thể tích bể \(V=a\cdot 2a\cdot c=2{{a}^{2}}c=288\) (1)
c) Từ (1) \(\Rightarrow c=\frac{144}{{{a}^{2}}}\)
nên \(S=2{{a}^{2}}+6a\cdot \frac{144}{{{a}^{2}}}=2{{a}^{2}}+\frac{864}{a}\).
Xét hàm số \(S(a)=2{{a}^{2}}+\frac{864}{a}\Rightarrow {{S}^{\prime }}(a)=4a-\frac{864}{{{a}^{2}}}\).
\({{S}^{\prime }}(a)=0\Leftrightarrow 4a-\frac{864}{{{a}^{2}}}=0\Leftrightarrow {{a}^{3}}=216\Leftrightarrow a=6\).
Bảng biến thiên của hàm số \(S(a)=2{{a}^{2}}+\frac{864}{a}(a>0)\)
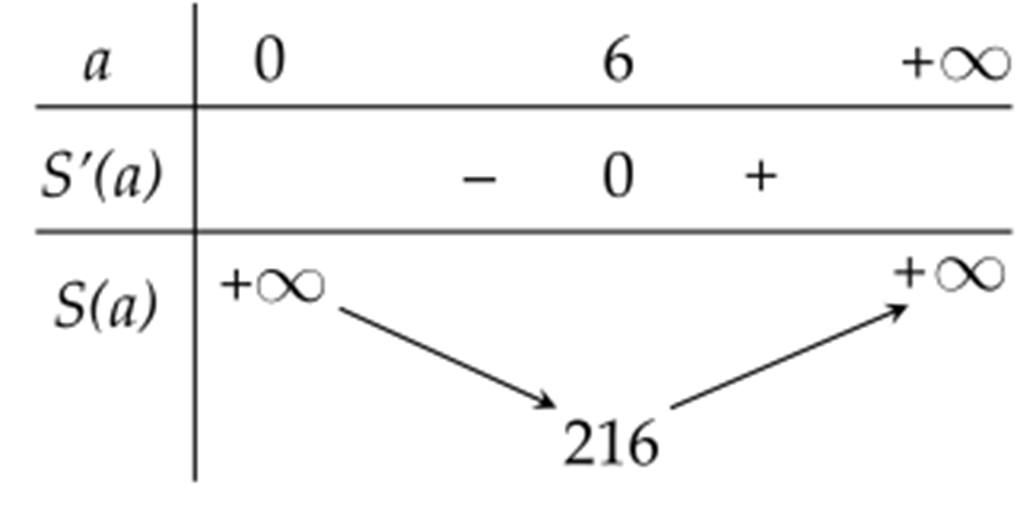
d) \({{S}_{\min }}=216~{{\text{m}}^{2}}\), khi đó chi phí thấp nhất là \(216 . 500000\) = \(108\) triệu đồng.
Cho hàm số \(y=f(x)=\sqrt{x-1}+\sqrt{9-x}\)
Tập xác định của hàm số \(y=f(x)\) là \(D=(1;9)\)
\({{f}^{\prime }}(5)=0\)
Hàm số \(y=f(x)\) đạt giá trị lớn nhất tại \(x=1\)
Tập giá trị của hàm số \(y=f(x)\) là \(T=(2\sqrt{2};4)\)
Tập xác định: \(D=(1;9)\).
\({{y}^{\prime }}=\frac{1}{2\sqrt{x-1}}-\frac{1}{2\sqrt{9-x}}=0\)
\(\Leftrightarrow \sqrt{9-x}=\sqrt{x-1}\)
\(\Leftrightarrow 9-x=x-1\Leftrightarrow x=5\) (thoả mãn).
\(f(1)=f(9)=2\sqrt{2};f(5)=4\)
Vậy tập giá trị là \(T=(2\sqrt{2};4)\).
26

Gọi \(\overrightarrow{{{F}_{1}}},\overrightarrow{{{F}_{2}}},\overrightarrow{{{F}_{3}}}\) là ba lực tác động vào vật đặt tại điểm O lần lượt có độ lớn là 25N, 12N, 4N.
Vẽ \(\overrightarrow{OA}=\overrightarrow{{{F}_{1}}};\overrightarrow{OB}=\overrightarrow{{{F}_{2}}};\overrightarrow{OC}=\overrightarrow{{{F}_{3}}}\)
Dựng hình bình hành OADB và hình bình hành ODE).
Hợp lực tác động vào vật là
\(\begin{array}{*{35}{l}} \vec{F}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC} \\ =\overrightarrow{OD}+\overrightarrow{OC}=\overrightarrow{OE} \\ \end{array}\)
Áp dụng định lí côsin trong tam giác OBD, ta có
\(O{{D}^{2}}=B{{D}^{2}}+O{{B}^{2}}-2\cdot BD\cdot OB\cdot \cos \widehat{OBD}\)
\(=O{{A}^{2}}+O{{B}^{2}}+2\cdot OA\cdot OB\cdot \cos {{100}^{{}^\circ }}\)
Vì \(OC\bot (OADB)\) nên \(OC\bot OD\), suy ra ODEC là hình chữ nhật.
Do đó tam giác ODE vuông tại D.
Ta có \(O{{E}^{2}}=O{{C}^{2}}+O{{D}^{2}}=O{{C}^{2}}+O{{A}^{2}}+O{{B}^{2}}+2\cdot OA\cdot OB\cdot \cos {{100}^{{}^\circ }}\).
Suy ra \(OE=\sqrt{O{{C}^{2}}+O{{A}^{2}}+O{{B}^{2}}+2\cdot OA\cdot OB\cdot \cos {{100}^{{}^\circ }}}\) \(=\sqrt{{{4}^{2}}+{{25}^{2}}+{{12}^{2}}+2\cdot 25\cdot 12\cdot \cos {{100}^{{}^\circ }}}\approx 26,092.\)
Vậy độ lớn của hợp lực là \(F=OE\approx 26~\text{N}\).

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Địa Lí 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026
ĐĂNG KÝ GÓI THI VIP
- Truy cập hơn 100K đề thi thử và chính thức các năm
- 2M câu hỏi theo các mức độ: Nhận biết – Thông hiểu – Vận dụng
- Học nhanh với 10K Flashcard Tiếng Anh theo bộ sách và chủ đề
- Đầy đủ: Mầm non – Phổ thông (K12) – Đại học – Người đi làm
- Tải toàn bộ tài liệu trên TaiLieu.VN
- Loại bỏ quảng cáo để tăng khả năng tập trung ôn luyện
- Tặng 15 ngày khi đăng ký gói 3 tháng, 30 ngày với gói 6 tháng và 60 ngày với gói 12 tháng.