Trắc nghiệm Khái niệm về mặt tròn xoay Toán Lớp 12
-
Câu 1:
Cho hình vuông (ABCD ) cạnh bằng 2. Gọi (M ) là trung điểm (AB ). Cho tứ giác (AMCD ) và các điểm trong của nó quay quanh trục (AD ) ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
A. 7π37π3
B. 7π67π6
C. 14π314π3
D. 7π97π9
-
Câu 2:
Một que kem ốc quế gồm hai phần: phần kem có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình cầu và hình nón có bán kính bằng nhau; biết rằng nếu kem tan chảy hết thì sẽ làm đầy phần ốc quế. Biết thể tích phần kem sau khi tan chảy chỉ bằng 75% thể tích kem đóng băng ban đầu. Gọi h và r lần lượt là chiều cao và bán kính của phần ốc quế. Tính tỉ số hrhr
A. hr=3hr=3
B. hr=1hr=1
C. hr=2hr=2
D. hr=4hr=4
-
Câu 3:
Cho hình nón đỉnh S, tâm đáy là O, góc ở đỉnh là 1350. Trên đường tròn đáy lấy điểm A cố định và điểm M di động. Tìm số vị trí M để diện tích SAM đạt giá trị lớn nhất
A. 4
B. 3
C. 2
D. 1
-
Câu 4:
Cho mặt cầu tâm (O ) bán kính (R ). Xét mặt phẳng (P) thay đổi cắt mặt cầu theo giao tuyến là đường tròn (C). Hình nón (N ) có đỉnh (S ) nằm trên mặt cầu, có đáy là đường tròn (C) và có chiều cao h (h > R ). Tìm (h ) để thể tích khối nón được tạo nên bởi (N) có giá trị lớn nhất.
A. h=R√3h=R√3
B. h=R√2h=R√2
C. h=4R3h=4R3
D. h=2R3h=2R3
-
Câu 5:
Cho hình nón có diện tích xung quanh bằng 3πa23πa2 và bán kính đáy bằng (a ). Tính độ dài đường sinh (l ) của hình nón đã cho.
A. l=√5a2l=√5a2
B. l=2√2al=2√2a
C. l=3a2l=3a2
D. 3a3a
-
Câu 6:
Người ta đặt được vào một hình nón hai khối cầu có bán kính lần lượt là a và 2a sao cho các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và khối cầu lớn tiếp xúc với đáy của hình nón. Bán kính đáy của hình nón đã cho là:
A. 8a38a3
B. 4√2a4√2a
C. 2√2a2√2a
D. 4a34a3
-
Câu 7:
Công thức tính thể tích khối nón biết diện tích đáy Sd và đường sinh l là:
A. V=13Sd.lV=13Sd.l
B. V=13Sd√h2−r2V=13Sd√h2−r2
C. V=13Sd√l2−r2V=13Sd√l2−r2
D. V=Sd√h2−r2V=Sd√h2−r2
-
Câu 8:
Khối nón có chiều cao bằng bán kính đáy và có thể tích bằng (9π9π ), chiều cao của khối nón đó bằng:
A. 2
B. 3
C. 4
D. 5
-
Câu 9:
Thiết diện qua trục của một khối nón là một tam giác vuông cân và có cạnh góc vuông bằng a√2a√2 Thể tích (V ) của khối nón bằng:
A. πa3√33πa3√33
B. πa33πa33
C. 4πa334πa33
D. 44
-
Câu 10:
Hình nón (N) có thiết diện qua trục là tam giác đều có cạnh bằng 4. Diện tích toàn phần của (N) bằng
A. 3π.
B. 8π.
C. 12π.
D. 9π
-
Câu 11:
Hình nón có thiết diện qua trục là tam giác đều cạnh (a = 3 ). Tính độ dài đường cao của hình nón.
A. 44
B. 3√323√32
C. 22
D. 3√343√34
-
Câu 12:
Cho tam giác ABO vuông tại O, có góc (góc BAO = 300,AB = a ) . Quay tam giác ABO quanh trục AO ta được một hình nón có diện tích xung quanh bằng:
A. πa2√34πa2√34
B. 2πa32πa3
C. πa22πa22
D. πa24πa24
-
Câu 13:
Cho hình nón có đường kính đường tròn đáy bằng (2a, ) chiều cao bằng (a. ) Khi đó thể tích khối nón bằng:
A. 4πa334πa33
B. 4πa34πa3
C. πa3πa3
D. πa33πa33
-
Câu 14:
Cho khối nón có độ dài đường cao bằng (2a ) và bán kính đáy bằng (a. ) Thể tích của khối nón đã cho bằng:
A. 2πa332πa33
B. πa33πa33
C. 4πa334πa33
D. 2πa352πa35
-
Câu 15:
Thể tích khối nón có bán kính đáy r = 2cm và h = 3cm là:
A. 4πcm34πcm3
B. πcm3πcm3
C. 2πcm32πcm3
D. 6πcm36πcm3
-
Câu 16:
Cho khối nón có độ dài đường sinh bằng (2a ) và bán kính đáy bằng (a ). Thể tích của khối nón đã cho bằng
A. √3πa33√3πa33
B. √3πa32√3πa32
C. √3πa34√3πa34
D. √3πa35√3πa35
-
Câu 17:
Thể tích khối nón có bán kính đáy (r ), độ dài đường sinh (l ) là:
A. V=13πr√l2−r2V=13πr√l2−r2
B. V=13πr2lV=13πr2l
C. V=13πr2√l2−r2V=13πr2√l2−r2
D. V=13πr√l2+r2V=13πr√l2+r2
-
Câu 18:
Công thức tính thể tích khối nón có bán kính đáy (r ), độ dài đường sinh (l ) và chiều cao (h ) là:
A. V=13πrlV=13πrl
B. V=13πr2lV=13πr2l
C. V=13πr2hV=13πr2h
D. V=13πrhV=13πrh
-
Câu 19:
Cho hình nón có bán kính đáy bằng 4a và chiều cao bằng 3a. Diện tích toàn phần của hình nón bằng:
A. 18πa2
B. 12πa2
C. 36πa2
D. 20πa2
-
Câu 20:
Cho hình nón có các kích thước (r = 1;h = 2 ) với (r,h ) lần lượt là bán kính đáy và độ dài đường cao hình nón. Diện tích toàn phần hình nón là:
A. ππ
B. (√5+2)π(√5+2)π
C. (√5+3)π(√5+3)π
D. (√5+1)π(√5+1)π
-
Câu 21:
Cho hình nón có độ dài đường sinh bằng 5, bán kính bằng 3. Diện tích toàn phần của hình nón bằng:
A. 15π
B. 48π
C. 39π
D. 24π
-
Câu 22:
Cho hình nón S có bán kính R=a√2R=a√2, góc ở đỉnh bằng 600. Diện tích toàn phần của hình nón bằng :
A. 8πa28πa2
B. 6πa26πa2
C. 2πa22πa2
D. 4πa24πa2
-
Câu 23:
Cho hình nón có các kích thước r = 1cm;l = 2cm với r,l lần lượt là bán kính đáy và độ dài đường sinh hình nón. Diện tích toàn phần hình nón là:
A. 2π(cm2)
B. 4π(cm2)
C. 3π(cm2)
D. 6π(cm2)
-
Câu 24:
Công thức tính diện tích toàn phần hình nón có bán kính đáy (r ), độ dài đường cao (h ) và độ dài đường sinh (l ) là:
A. Stp=πrl+πr2Stp=πrl+πr2
B. Stp=πrl+2πr2Stp=πrl+2πr2
C. Stp=πrh+πr2Stp=πrh+πr2
D. Stp=2πrhStp=2πrh
-
Câu 25:
Cho hình nón có bán kính đường tròn đáy bằng R, chiều cao bằng h, độ dài đường sinh bằng l. Khẳng định nào sau đây đúng?
A. R2=l2+h2R2=l2+h2
B. l=√R2+h2l=√R2+h2
C. l=√R2−h2l=√R2−h2
D. h=√R2−l2h=√R2−l2
-
Câu 26:
Gọi (r,l,h ) lần lượt là bán kính đáy, độ dài đường sinh và chiều cao của hình nón. Chọn mệnh đề đúng:
A. r=hr=h
B. h=lh=l
C. r2=h2−l2r2=h2−l2
D. l2=r2+h2l2=r2+h2
-
Câu 27:
Mệnh đề nào dưới đây là sai?
A. Góc giữa hai đường sinh đối xứng qua trục của mặt nón bằng góc ở đỉnh của mặt nón.
B. Diện tích xung quanh của hình nón tròn xoay là giới hạn của diện tích xung quanh của hình chóp đều ngoại tiếp hình nón đó, khi số cạnh đáy tăng lên vô hạn
C. Diện tích xung quanh của hình nón bằng một nửa tích của chu vi đáy với độ dài đường sinh.
D. Diện tích xung quanh của hình nón tròn xoay là giới hạn của diện tích xung quanh của hình chóp đều nội tiếp hình nón đó, khi số cạnh đáy tăng lên vô hạn.
-
Câu 28:
Cho hình nón bán kính đáy r và diện tích xung quanh Sxq. Độ dài đường sinh l của hình nón là:
A. l=r.Sxqπl=r.Sxqπ
B. l=Sxq2πrl=Sxq2πr
C. l=Sxqπrl=Sxqπr
D. l=3Sxqπrl=3Sxqπr
-
Câu 29:
Cho hình nón có chiều cao (h = 4, ) bán kính đáy (r = 3. ) Diện tích xung quanh của hình nón đã cho bằng:
A. 20π
B. 10π
C. 15π
D. 30π
-
Câu 30:
Cho hình nón có bán kính đáy r=√3r=√3, độ dài đường sinh l = 4. Tính diện tích xung quanh của hình nón đó?
A. √39π√39π
B. 4√3π4√3π
C. 12π12π
D. 39π39π
-
Câu 31:
Diện tích xung quanh hình nón có bán kính đáy (r = 3cm ) và độ dài đường sinh (4cm ) là:
A. 12(m2)
B. 12π(cm3)
C. 12π(cm2)
D. 4π(cm2)
-
Câu 32:
Diện tích xung quanh của hình nón có bán kính đường tròn đáy (R ) và chiều cao (h ) bằng:
A. Sxq=13πR2hSxq=13πR2h
B. Sxq=πR√R2+h2Sxq=πR√R2+h2
C. Sxq=πR√R2−h2Sxq=πR√R2−h2
D. Sxq=πRhSxq=πRh
-
Câu 33:
Công thức tính diện tích xung quanh hình nón có bán kính đáy (r ) và độ dài đường sinh (l ) là
A. Sxq=13πrlSxq=13πrl
B. Sxq=πr2lSxq=πr2l
C. Sxq=πrl+πr2Sxq=πrl+πr2
D. Sxq=πrlSxq=πrl
-
Câu 34:
Cho hình (H) dưới đây: Quay hình (H) quanh trục đối xứng của nó ta được:
A. Hình trụ nội tiếp hình nón.
B. Hình nón nội tiếp hình trụ.
C. Hình cầu ngoại tiếp hình trụ.
D. Hình cầu ngoại tiếp hình nón.
-
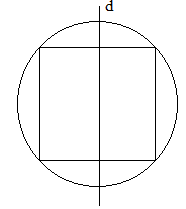
Câu 35:
Cho hình vẽ sau, chọn mệnh đề sai:
A. Mặt cầu ngoại tiếp hình nón
B. Hình nón nội tiếp hình trụ
C. Hình trụ nội tiếp mặt cầuM
D. Hình nón nội tiếp mặt cầu
-
Câu 36:
Cho hình (H) bao gồm tam giác (ABC ) đều nội tiếp đường tròn (C). Quay hình (H) quanh trục đối xứng của nó ta được:
A. Hình nón nội tiếp hình cầu
B. Hình trụ nội tiếp hình cầu
C. Hình nón ngoại tiếp hình cầu
D. Hình cầu nội tiếp hình trụ
-
Câu 37:
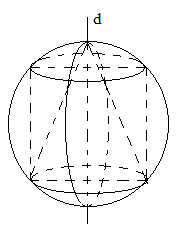
Khi quay hình vẽ dưới đây quanh trục đối xứng là đường thẳng (d ) thì ta được:
A. Hình trụ ngoại tiếp mặt cầu
B. Mặt cầu ngoại tiếp hình trụ
C. Hình nón nội tiếp mặt cầu
D. Hình trụ ngoại tiếp hình nón.
-
Câu 38:
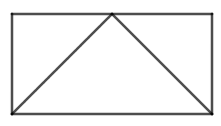
Nếu cắt hình trụ bởi mặt phẳng đi qua trục thì ta được thiết diện là:
A. Hình vuông
B. Hình tròn
C. Hình elip
D. Hình chữ nhật
-
Câu 39:
Cho hình trụ có trục (ΔΔ) và bán kính (R ). Khi cắt hình trụ bởi mặt phẳng (αα) song song với (ΔΔ) và cách (ΔΔ ) một khoảng d(Δ;(α))=k<Rd(Δ;(α))=k<R thì ta được thiết diện là:
A. Hình chữ nhật
B. Hình tròn
C. Hình elip
D. Đường sinh
-
Câu 40:
Cho đường thẳng (ΔΔ) cố định và đường thẳng (d//ΔΔ ). Quay (d ) quanh (Δ ) ta được:
A. Mặt nón
B. Mặt trụ
C. Mặt cầu
D. Đường thẳng
-
Câu 41:
Cho hai đường thẳng (d ) và (Δ ), điều kiện nào sau đây của (d ) và (Δ) thì khi quay (d ) quanh (Δ) ta được một mặt trụ?
A. d≡Δ
B. d//Δ
C. d chéo Δ
D. d⊥Δ
-
Câu 42:
Cho hình chữ nhật (ABCD ). Gọi (M,N ) lần lượt là trung điểm các cạnh (AB,CD ). Quay hình chữ nhật quanh trục (MN ) ta được hình trụ có bán kính đáy là:
A. MN
B. AB
C. CM
D. AM
-
Câu 43:
Khi quay hình chữ nhật (MNPQ ) quanh đường thẳng (AB ) với (A,B ) lần lượt là trung điểm của (MN,PQ ) ta được một hình trụ có đường kính đáy:
A. MA
B. AB
C. MQ
D. MN
-
Câu 44:
Nếu cắt mặt trụ tròn xoay bởi một mặt phẳng tạo với trục một góc 45 0 thì ta được:
A. Đường tròn
B. Hình chữ nhật ình chữ nhật
C. Hình thang cân
D. Elip
-
Câu 45:
Nếu cắt mặt trụ tròn xoay bởi một mặt phẳng tạo với trục một góc α(00<α<900) thì ta được:
A. Đường tròn
B. Hình chữ nhật
C. Hình thang cân
D. Elip
-
Câu 46:
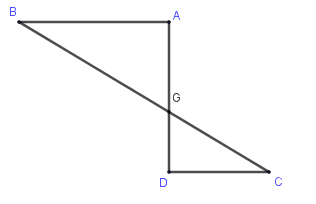
Số hình nón có được khi quay hình sau quanh trục (BC ) là:
A. 1
B. 2
C. 3
D. 4
-
Câu 47:
Quay hình chữ nhật (ABCD ) quanh mỗi cạnh (AB,CD ) thì ta được hai hình trụ có
A. Cùng chiều cao
B. Cùng tâm đáy
C. Không cùng bán kính đáy
D. Không cùng diện tích đáy
-
Câu 48:
Khi quay hình chữ nhật (ABCD ) quanh các cạnh nào dưới đây ta được hai hình trụ có cùng chiều cao?
A. AB và AD
B. AC và AB
C. BD và AC
D. BC và AD
-
Câu 49:
Cho hình chữ nhật (ABCD ), khi quay hình chữ nhật quanh cạnh (AB ) thì (CD ) được gọi là:
A. Đường sinh
B. Đường kính đáy
C. Chu vi đáy
D. Bán kính đáy.
-
Câu 50:
Cho hình chữ nhật (ABCD ), khi quay hình chữ nhật quanh cạnh (AD ) thì (CD ) được gọi là:
A. Chiều cao
B. Đường kính đáy
C. Chu vi đáy
D. Bán kính đáy.