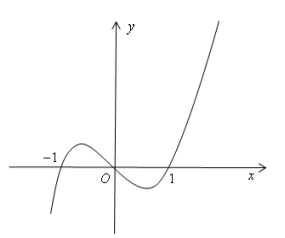
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình sau.
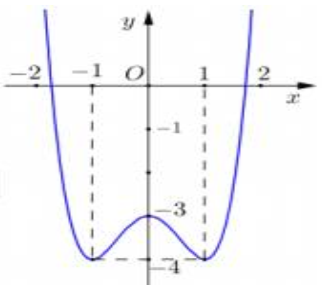
Tìm m để phương trình \(f\left(\mathrm{e}^{x^{2}}\right)=m^{2}+5 m\) có hai nghiệm thực phân biệt.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(t=\mathrm{e}^{x^{2}} \geq \mathrm{e}^{0}=1\) . Khi đó ứng với mỗi nghiệm t > 1, ta được hai nghiệm x .
Từ đồ thị của hàm số y=f(x), ta thấy phương trình \(f(t)=m^{2}+5 m\) có đúng một nghiệm t > 1 khi và chỉ khi \(m^{2}+5 m>-4 \Leftrightarrow\left[\begin{array}{l} m<-4 \\ m>-1 \end{array}\right.\)
Câu hỏi liên quan
-
Hàm số \(y=\frac{1}{3} x^{3}+(m+1) x^{2}-(m+1) x+1\) đồng biến trên tập xác định của nó khi?
-
Cho hàm số \(y = \frac{{ - x + 5}}{{x + 2}}\). Mệnh đề nào sau đây là đúng?
-
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(f(x)=\frac{x+m^{2}}{x+3 m+4}\)đồng biến trên khoảng (-10;5)?
-
Các khoảng nghịch biến của hàm số \(y=\frac{2x+1}{x-1}\) là:
-
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y=f'(x)\) như hình bên dưới.
Hỏi hàm số \(g(x)=f(1-x)+\frac{x^{2}}{2}-x\) nghịch biến trên khoảng nào? -
Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(3\sqrt {x - 1} + m\sqrt {x + 1} = 2\sqrt[4]{{{x^2} - 1}}\) có hai nghiệm thực?
-
Để giảm nhiệt độ trong phòng từ 280C , một hệ thống làm mát được phép hoạt động trong 10 phút. Gọi T (đơn vị 0C ) là nhiệt độ phòng ở phút thứ t được cho bởi công thức \(T=-0,008 t^{3}-0,16 t+28 \text { với } t \in[1 ; 10]\) . Tìm nhiệt độ thấp nhất trong phòng đạt được trong\ thời gian 10 phút kể từ khi hệ thống làm mát bắt đầu hoạt động.
-
Cho hàm số y=f(x) có đạo hàm \(f^{\prime}(x)=x(x-1)^{2}(x+3), \forall x \in \mathbb{R}\) . Hàm số y=f(x) nghịch biến trên khoảng
-
Cho hàm số \(y = \frac{{x – 2}}{{x + 1}}\). Mệnh đề nào dưới đây đúng?
-
Tìm m để hàm số \(y=\frac{x-m}{x+1}\) đồng biến trên từng khoảng xác định của chúng.
-
Tập hợp tất cả các giá trị thực của tham số m để hàm số \(y = {x^3} – 3{x^2} + \left( {1 – m} \right)x\) đồng biến trên khoảng \(\left( {2; + \infty } \right)\) là
-
Tìm các giá trị thực của m để hàm số \(y=\frac{1}{3} x^{3}-2 x^{2}+m x-1\) đồng biến trên R.
-
Cho hàm số \(y=f(x)=x^{3}+m x^{2}+2 x+3 \text { . }\)Tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên R là?
-
Tập nghiệm của bất phương trình: \(\sqrt {5x - 1} + \sqrt {x + 3} \ge 4\) có bao nhiêu giá trị nguyên trong ( 0; 2008]
-
Cho phương trình x3- 3x2+ 1- m = 0 (1) . Điều kiện của tham số m để (1) có ba nghiệm phân biệt thỏa mãn x1 < 1< x2 < x3 khi
-
Hàm số \(y = {x^3} + 8{x^2} + 3x - 2\) đồng biến trên khoảng nào sau đây?
-
Cho hàm số y=f(x) có đạo hàm \(f^{\prime}(x)=x(x-1)^{2}(x-2)\). Hỏi hàm số \(y=f\left(\frac{5 x}{x^{2}+4}\right)\) đồng biến trên khoảng nào dưới đây?
-
Cho hàm số \(y=\frac{1}{3}x^3-\frac{1}{2}x^2-12x-1\). Mệnh đề nào sau đây đúng ?
-
Hàm số nào sau đây đồng biến trên R.
-
Hàm số y = x3 – 3x2 – 9x + 1 đồng biến trên mỗi khoảng:
