Đề thi thử Đánh giá năng lực ĐHQG Hà Nội năm 2025 - Đề 6 - Đề 1
50 câu hỏi 60 phút
Cho cấp số nhân \(\left(u_{n}\right)\) có \(u_{1}=3\), công bội \(q=2\). Khi đó \(u_{5}\) bằng
24
11
48
9
Công thức số hạng tổng quát của cấp số nhân: \(u_{n}=u_{1} \cdot q^{n-1}\).
Do đó \(u_{5}=3.2^{4}=48\).
Danh sách câu hỏi:
Câu 1:
Cho cấp số nhân \(\left(u_{n}\right)\) có \(u_{1}=3\), công bội \(q=2\). Khi đó \(u_{5}\) bằng
Công thức số hạng tổng quát của cấp số nhân: \(u_{n}=u_{1} \cdot q^{n-1}\).
Do đó \(u_{5}=3.2^{4}=48\).
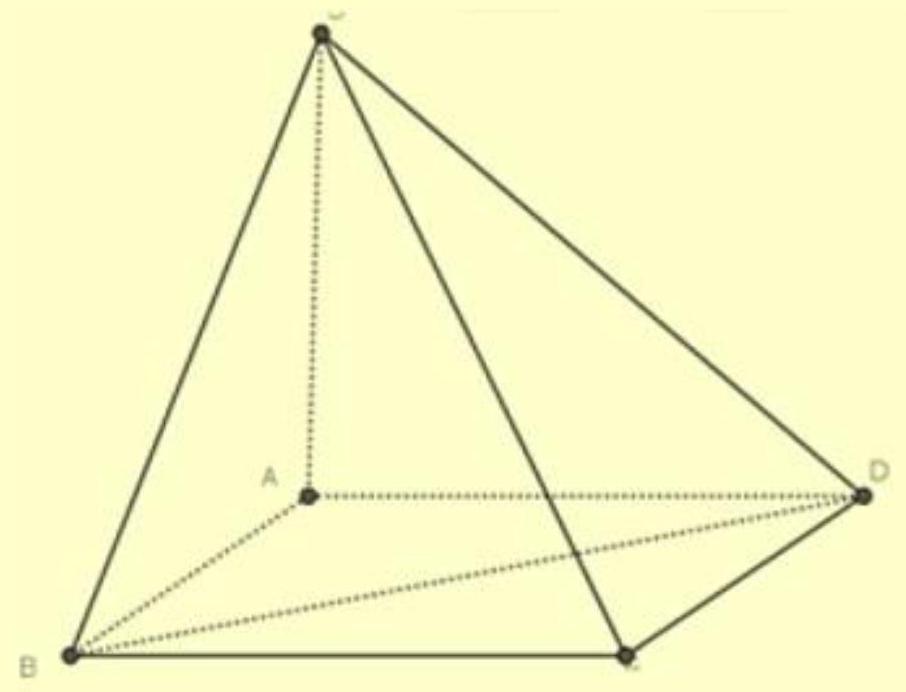
\(\triangle S B C\) vuông tại \(B\) do \(B C \perp(S A B) \Rightarrow B C \perp S B\)
\(\triangle S C D\) vuông tại \(C\) do \(C D \perp(S A D) \Rightarrow C D \perp S D\)
\(\triangle S A B\) vuông tại A do \(S A \perp A B\)
Độ chính xác \(d=0,001\) nên ta quy tròn số gần đúng \(a=5,2463\) đến hàng phần trăm và ta được số gần đúng là \(a \approx 5,25\).
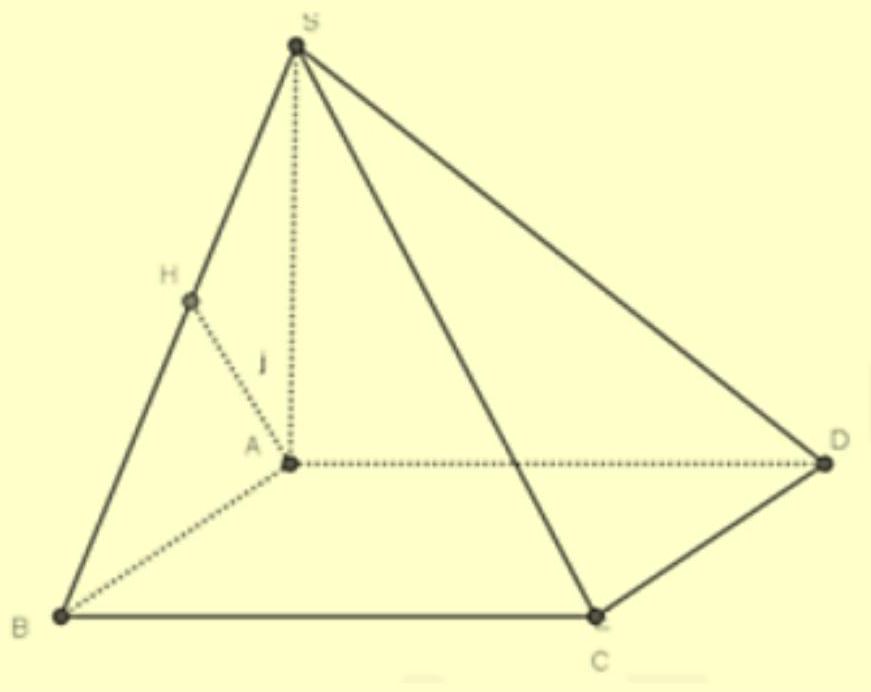
Có \(\left\{\begin{array}{l}B C \perp S A B C \perp A B\end{array} \Rightarrow B C \perp(S A B)\right.\) mà \(A H \subset(S A B)\) nên \(B C \perp A H\).
Có \(\left\{\begin{array}{l}A H \perp S B A H \perp B C\end{array} \Rightarrow A H \perp(S B C)\right.\).
\(\lim _{x \rightarrow 1} \frac{\sqrt{x+8}-3}{x-2}=\lim _{x \rightarrow 1} \frac{\sqrt{1+8}-3}{1-2}=0\)
Câu 7:
Cho 2 số thực dương \(a, b\) thỏa mãn \(a+b=5 a b\). Khẳng định nào sau đây là khẳng định đúng ?
Câu 33:
Tổng các giá trị m nguyên để phương trình sau \(\sin x \cos x-m(\sin x+\cos x)+1=0\) có nghiệm
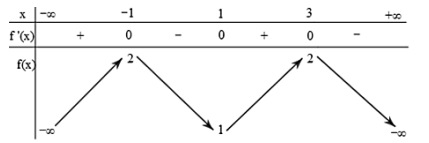
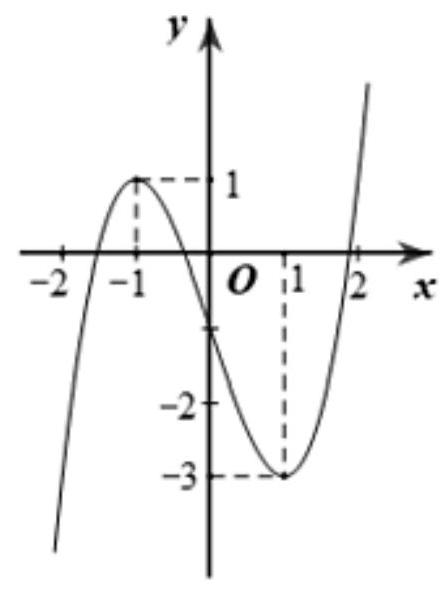
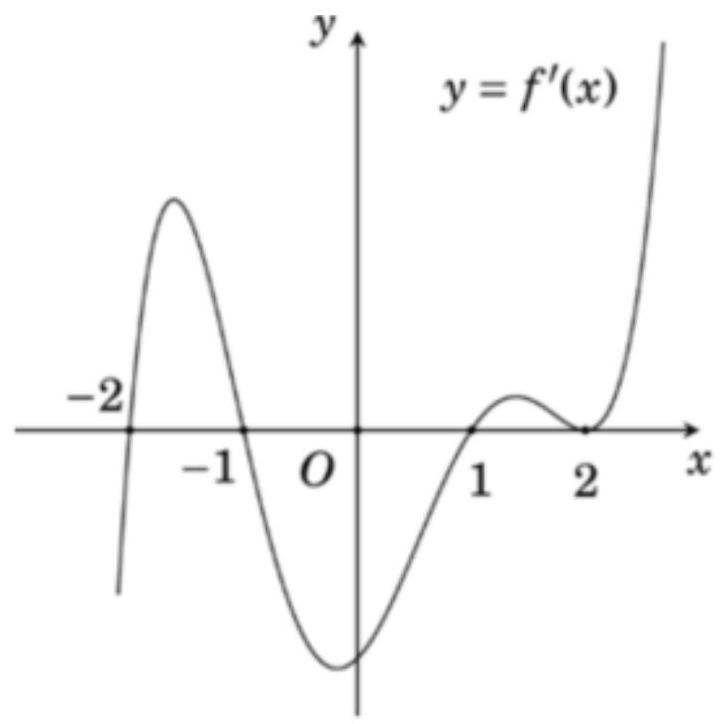
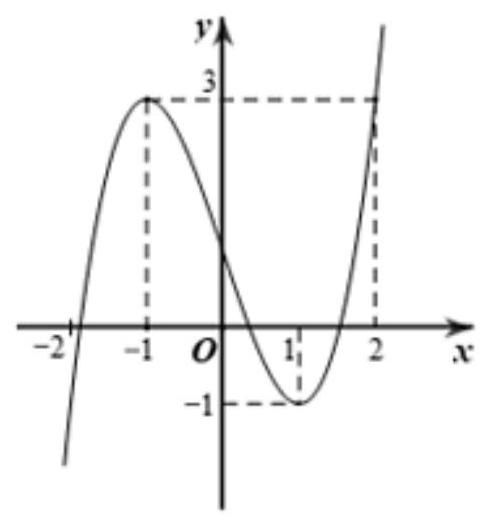 Xét hàm số \(g(x)=f\left(2 x^{3}+x-1\right)+m\). Với giá trị nào của \(m\) thì giá trị nhỏ nhất của \(g(x)\) trên đoạn \([0;1]\) bằng \(- 20\)
Xét hàm số \(g(x)=f\left(2 x^{3}+x-1\right)+m\). Với giá trị nào của \(m\) thì giá trị nhỏ nhất của \(g(x)\) trên đoạn \([0;1]\) bằng \(- 20\)