Đề thi thử Đánh giá năng lực ĐHQG Hà Nội năm 2025 - Đề 4 - Đề 1
50 câu hỏi 60 phút
Cho hàm số \(y=\left\{\begin{array}{l}x, k h i: x \geq 0 \\-x, k h i: x<0\end{array}\right.\). Khẳng định nào dưới đây đúng?
Hàm số không có đạo hàm tại \(x=0\)
\(y_{(0)}^{\prime}=1\)
\(y_{(0)}^{\prime}=0\)
\(y_{(0)}^{\prime}=-1\)
Ta có: \(y^{\prime}=\left\{\begin{array}{l}1, k h i: x \geq 0 \\ -1, k h i: x<0\end{array}\right.\)
Do \(\left\{\begin{array}{l}y_{\left(0^{+}\right)}^{\prime}=1 \\y_{\left(0^{-}\right)}^{\prime}=-1\end{array}\right.\)
\(\Rightarrow\) Hàm số không có đạo hàm tại \(x=0\).
Danh sách câu hỏi:
Ta có: \(y^{\prime}=\left\{\begin{array}{l}1, k h i: x \geq 0 \\ -1, k h i: x<0\end{array}\right.\)
Do \(\left\{\begin{array}{l}y_{\left(0^{+}\right)}^{\prime}=1 \\y_{\left(0^{-}\right)}^{\prime}=-1\end{array}\right.\)
\(\Rightarrow\) Hàm số không có đạo hàm tại \(x=0\).
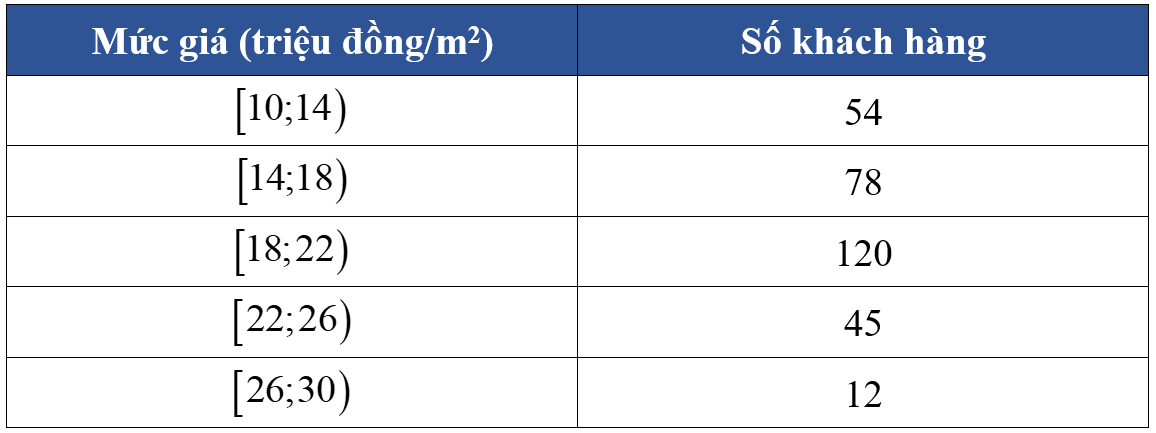
Số trung bình cộng thời gian chạy của học sinh là:
\(\bar{x}=\frac{8,3 \cdot 2+8,4 \cdot 3+8,5 \cdot 9+8,7 \cdot 5+8,8 \cdot 1}{20}=8,53.\)
\(y=\sin \left(\frac{2}{5} x\right) \cdot \cos \left(\frac{2}{5} x\right)=\frac{1}{2} \sin \left(\frac{4}{5} x\right)\)
Hàm số trên có chu kì là \(T=\frac{2 \pi}{|a|}=\frac{2 \pi}{\frac{4}{5}}=\frac{5 \pi}{2} =2,5\)
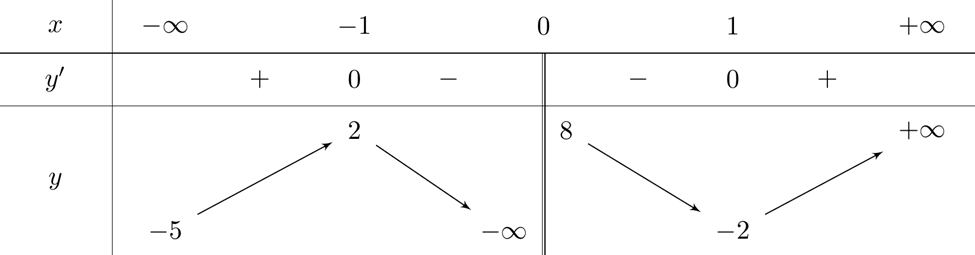
Số đường tiệm cận ngang: 1.
Số đường tiệm cận đứng: 1.
Tổng số đường tiệm cận ngang và tiệm cận đứng: 2.
\(F(t)=\int t x d t=x \int t d t=x \cdot \frac{t^2}{2}+C\)