Câu hỏi:
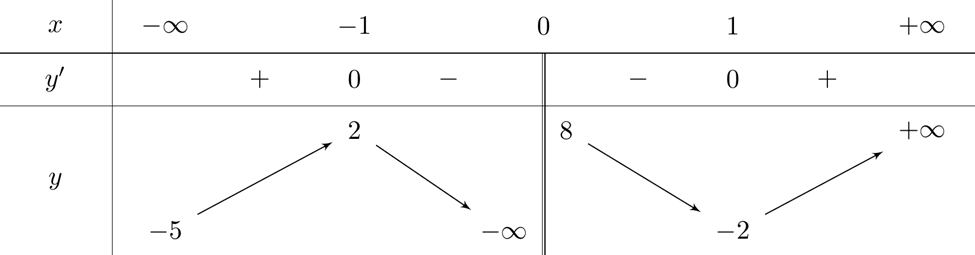
Cho hàm số \(y=f(x)\) là một hàm đa thức có bảng xét dấu \(f^{\prime}(x)\) như sau:
Số điểm cực trị của hàm số \(g(x)=f\left(-2 x^2+|x|\right)\).
Đáp án đúng: A
Ta có \(g(x)=f\left(-2 x^2+|x|\right)=f\left(-2|x|^2+|x|\right)\). Số điểm cực trị của hàm số \(h(|x|)\) bằng hai lần số điểm cực trị dương của hàm số \(h(x)\) cộng thêm 1 .
Xét hàm số
\(h(x)=f\left(-2 x^2+x\right) \Rightarrow h^{\prime}(x)=(-4 x+1) f^{\prime}\left(-2 x^2+x\right)=0 \Leftrightarrow\left[\begin{array}{l}x=\frac{1}{4} \\-2 x^2+x=-1 \\-2 x^2+x=1\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{l}x=\frac{1}{4} \\x=1 \\x=\frac{-1}{2}\end{array}\right.\)
Bảng xét dấu hàm số \(h(x)=f\left( -2{{x}^{2}}+x \right)\):
Hàm số \(h(x)=f\left( -2{{x}^{2}}+x \right)\) có 2 điểm cực trị dương.
Vậy hàm số \(g(x)=f\left(-2 x^2+|x|\right)=f\left(-2|x|^2+|x|\right)\) có 5 điểm cực trị.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Với cấu trúc mới lạ và đa dạng, Đề Thi Tham Khảo Đánh Giá Năng Lực Năm 2025 – ĐHQG Hà Nội – Đề Số 4 giúp thí sinh phát huy tối đa khả năng Giải Quyết Vấn Đề, Sáng Tạo và Tư Duy Định Lượng. Bài thi bao gồm ba phần chính: Toán Học Và Xử Lí Số Liệu, Văn Học - Ngôn Ngữ, Khoa Học/Tiếng Anh. Mỗi phần thi đều được thiết kế với các dạng câu hỏi phong phú, không chỉ đánh giá kiến thức lý thuyết mà còn kiểm tra khả năng phân tích dữ liệu, xử lý thông tin và vận dụng thực tế. Đây là lựa chọn hoàn hảo cho học sinh muốn tự tin chinh phục kỳ thi đánh giá năng lực.
Câu hỏi liên quan
Khi xe dừng hẳn thì vận tốc bằng 0.
Nên thời gian kể từ lúc đạp phanh đến lúc ô tô dừng hẳn là \(-2 t+10=0 \Leftrightarrow t=5(\mathrm{~s})\)
Quãng đường ô tô đi được từ lúc đạp phanh đến lúc ô tô dừng hẳn là
\(S_2=\int_0^5(-2 t+10) d t=\left.\left(-t^2+10 t\right)\right|_0 ^5=25 m\)
Như vậy trong 8 giây cuối thì có 3 giây ô tô đi với vận tốc \(10 \mathrm{~m} / \mathrm{s}\) và 5 giây ô tô chuyển động chậm dần đều.
Quãng đường ô tô đi được trong 3 giây trước khi đạp phanh là \(S_1=3.10=30 \mathrm{~m}\).
Vậy trong 8 giây cuối ô tô đi được quãng đường \(S=S_1+S_2=30+25=55 m\).
Quãng đường máy bay bay được với vận tốc 890km/h trong nửa giờ là:
\(S=v.t=890.\frac{1}{2}=445\,\,(\text{km}).\)
Vì máy bay duy trì hướng bay về phía nam nên toạ độ của vectơ biểu diễn độ dịch chuyển của chiếc máy bay trong nửa giờ đó với hệ toạ độ đã chọn là (0;445;0).
Đầu tiên, 9 con cá đói, mỗi con sẽ ăn 3 con cá đói khác để tạo thành 1 con cá no. Khi đó trong trò chơi còn lại 2 con cá đói và 9 con cá no.
Để số con cá no là tối đa thì 1 con cá đói sẽ ăn 1 con cá đói còn lại và 2 con cá no khác.
Khi đó, trong trò chơi sẽ không còn cá đói và có 8 con cá no.
Chọn 6 giờ là mốc thời gian. Khi đó \(A=150\).
Sau 3 giờ, số lượng vi khuẩn là 450 con nên \(t=3 ; S(3)=450\).
Từ đó ta có phương trình:
\(150 . e^{3 r}=450 \Leftrightarrow e^{3 r}=3 \Leftrightarrow r=\frac{\ln 3}{3} \approx 0,37.\)
Gọi \(t_1\) là thời điểm số lượng vi khuẩn gấp 9 lần ban đầu.
Khi đó: \(S\left(t_1\right)=1350\) con.
Ta có phương trình:
\(150.{{e}^{\frac{\ln 3}{3}.{{t}_{1}}}}=1350\Leftrightarrow {{e}^{\frac{\ln 3}{3}.{{t}_{1}}}}=9\Leftrightarrow \frac{\ln 3}{3}{{t}_{1}}=\ln 9\Leftrightarrow {{t}_{1}}=6.\)
Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026
