Đề thi thử Đánh giá năng lực ĐHQG Hà Nội năm 2025 - Đề 5 - Đề 1
50 câu hỏi 60 phút
Trong hệ trục tọa độ Oxy , cho đường thẳng \(d:\left\{\begin{array}{l}x=-4 t+1 \\ y=-2+3 t\end{array}\right.\). Một vectơ chỉ phương của \(d\) là:
\((1; 3)\)
\((-4;2)\)
\((4;-3)\)
\((-1; 3)\)
Một vectơ chỉ phương của \(d\) là \((-4; 3)\) hay \((4;-3)\).
Danh sách câu hỏi:
Một vectơ chỉ phương của \(d\) là \((-4; 3)\) hay \((4;-3)\).
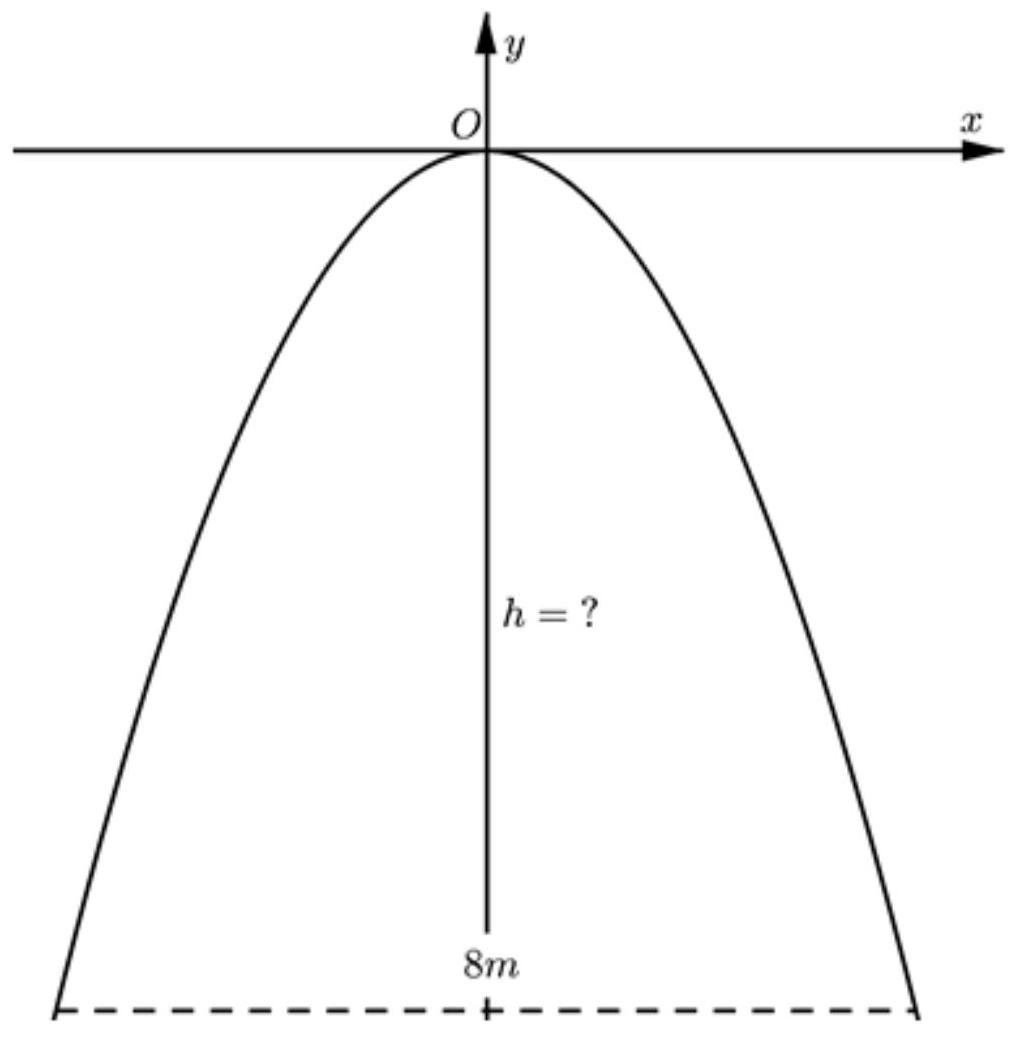
Khoảng cách từ chân cổng đến trục đối xứng Oy là \(\frac{8}{2}=4\). Hoành độ hai chân cổng là \(-4; 4\)
Tung độ chân cổng là: \(y=-\frac{1}{2} \cdot 4^{2}=-8\)
Vậy chiều cao của cổng là \(|-8|=8\) mét.
Để bất phương trình \(x^{2}-(m+2) x+8 m+1 \leq 0\) vô nghiệm thì \(x^{2}-(m+2) x+8 m+1>0, \forall x \in \mathbb{R}\).
\(\begin{align}& \Leftrightarrow\left\{\begin{array}{l}a=1>0 \\ \Delta=(m+2)^{2}-4(8 m+1)<0\end{array}\right. \\& \Leftrightarrow m^{2}+4 m+4-32 m-4<0 \\& \Leftrightarrow m^{2}-28 m<0 \\& \Leftrightarrow 0<m<28.\end{align}\)
Câu 4:
Số cách xếp 5 học sinh ngồi vào một dãy gồm 5 chiếc ghế sao mỗi ghế có đúng một học sinh ngồi là
Số cách xếp 5 học sinh ngồi vào một dãy gồm 5 chiếc ghế là: \(5!=120\) (cách).
Ta có: \(u_{n+1}=\sqrt{3 u_{n}^{2}+2} \Leftrightarrow u_{n+1}^{2}=3 u_{n}^{2}+2 \Leftrightarrow u_{n+1}^{2}+1=3\left(u_{n}^{2}+1\right)\).
Đặt \(v_{n}=u_{n}^{2}+1 \Rightarrow\left\{\begin{array}{l}v_{1}=2. \\ v_{n+1}=3 v_{n}.\end{array}\right.\)
Do \(\left(v_{n}\right)\) là cấp số nhân có \(v_{1}=2\) công bội \(q=3\) nên \(v_{n}=2.3^{n-1}\).
\(\Rightarrow u_{n}^{2}=2.3^{n-1}-1\).
Khi đó: \(S=2 \cdot\left(1+3^{1}+3^{2}+\ldots+3^{2022}\right)=3^{2023}-1\).
Ta có: \(S+1=3^{2023}\) có \(\left[\log 3^{2023}\right]+1=966\) (chữ số).
Do đó \(S\) có 966 hoặc 965 chữ số.
\(S\) có 965 chữ số khi \(S+1=10^{965} \Leftrightarrow 3^{2023}=10^{965}\) (vô lý do \(3^{2023}\) là số lẻ còn \(10^{965}\) là số chẵn).
Vậy số chữ số của \(S=966\) (chữ số).
Câu 27:
Cho hàm số \(y=\sqrt{2 x-x^{2}}\). Biết hàm số nghịch biến trên đoạn \((a; b)\), Tính \(a+2 b\)
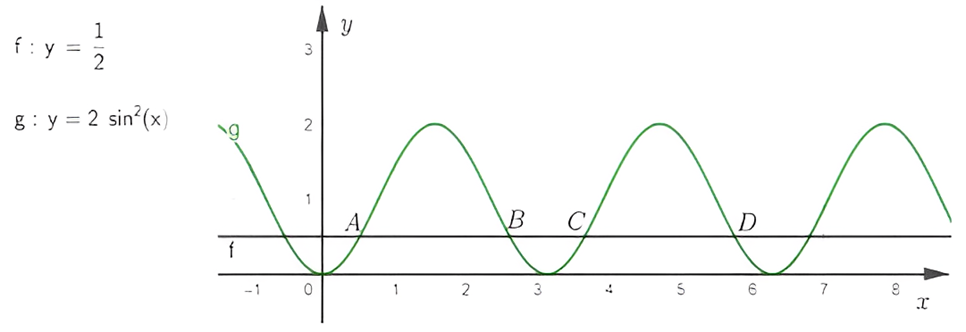
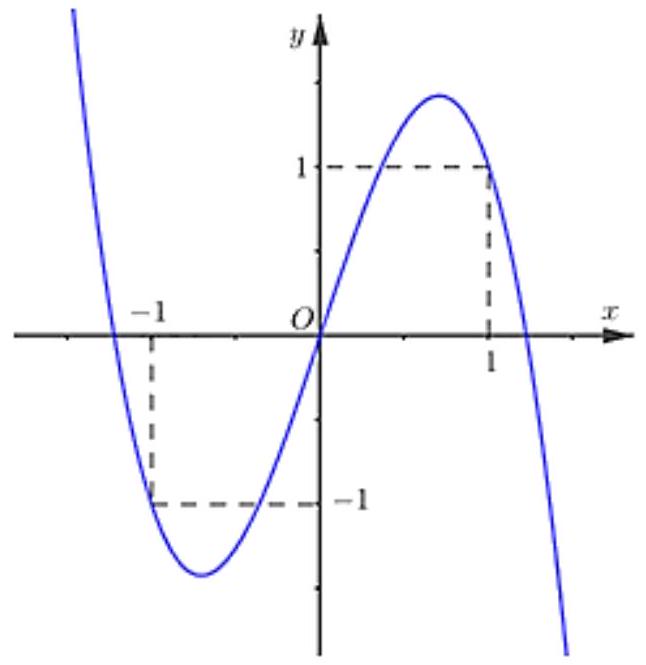 Hàm số \(y=\left|f(x)-\frac{x^{2}}{2}\right|\) có bao nhiêu điểm cực trị?
Hàm số \(y=\left|f(x)-\frac{x^{2}}{2}\right|\) có bao nhiêu điểm cực trị?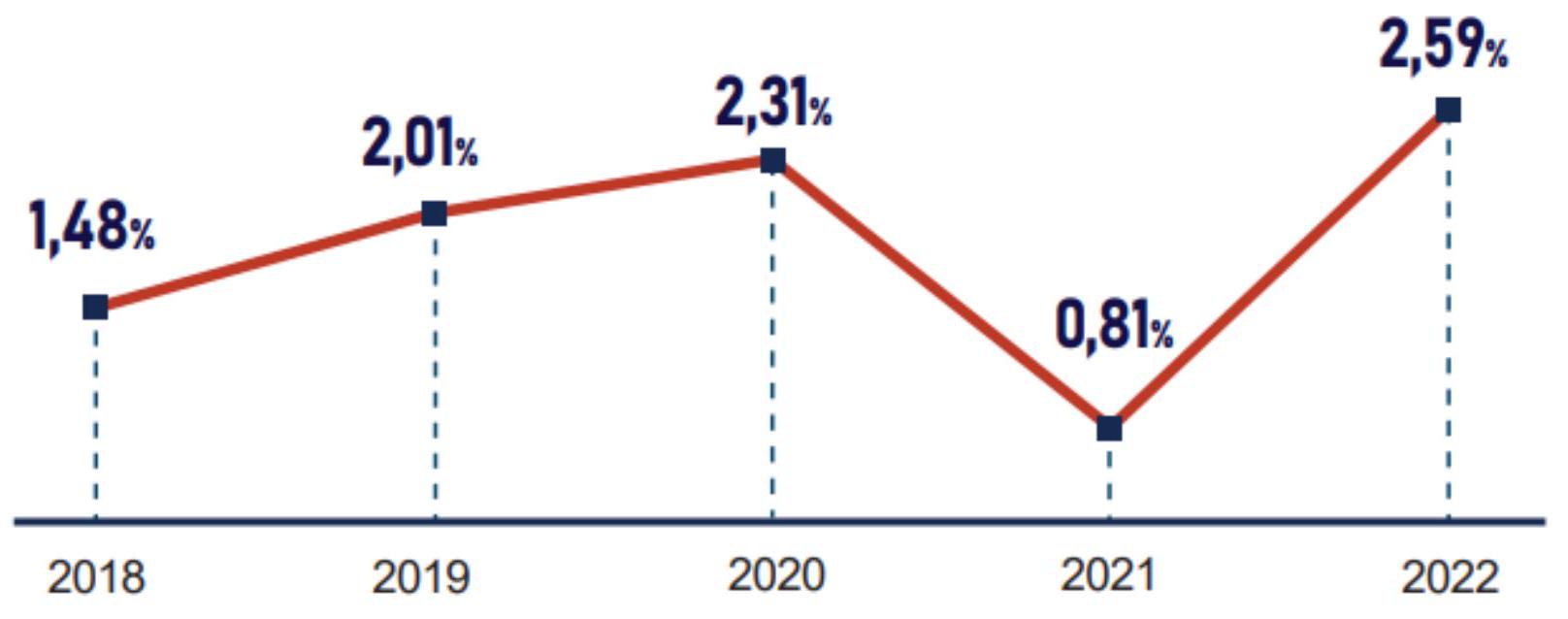 (Nguồn: Niêm giám thống kê 2022)
(Nguồn: Niêm giám thống kê 2022)