Câu hỏi:
Cho tứ diện \(ABCD\) có \(BCD\) là tam giác vuông tại đỉnh \(B\), cạnh \(C D=a, B D=\frac{a \sqrt{6}}{3}\), \(A B=A C=A D=\frac{a \sqrt{3}}{2}\). Tính cosin của góc nhị diện \([\mathrm{A}, \mathrm{BC}, \mathrm{D}]\).
Đáp án đúng: B
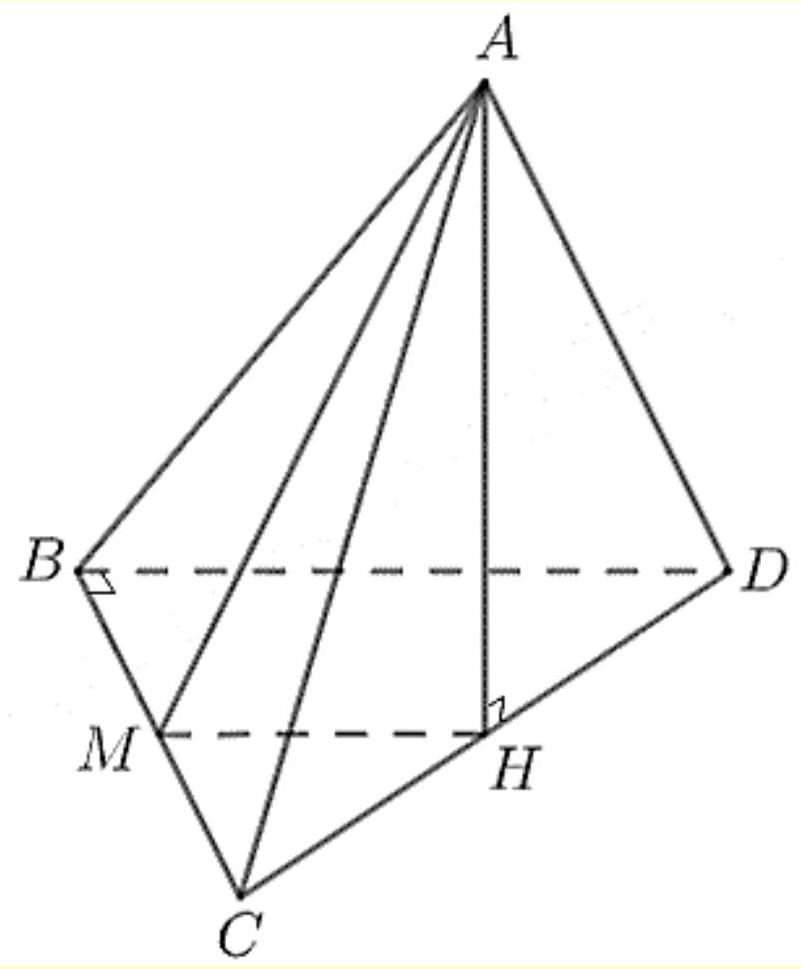
Gọi \(\mathrm{M}, \mathrm{H}\) lần lượt là trung điểm của \(\mathrm{BC}, \mathrm{CD}\).
Do \(\triangle B C D\) vuông tại \(B\) nên \(B H=C H=D H\) hay \(H\) là tâm đường tròn ngoại tiếp \(\triangle B C D\). Mà \(A B=A C=A D\) nên \(A H\) là đường cao kẻ từ \(A\) xuống \((B C D)\) hay \(A H \perp(B C D)\).
\(\Rightarrow A H \perp B C\) (1).
\(\mathrm{M}, \mathrm{H}\) là trung điểm của \(\mathrm{BC}, \mathrm{CD}\) nên MH là đường trung bình của \(\triangle B C D\)
\(\Rightarrow\left\{\begin{array}{l}M H=\frac{1}{2} B D=\frac{a \sqrt{6}}{6} \\ M H / / B D\end{array}\right.\).
Mà \(M D \perp B C\) nên \(M H \perp B C\). (2)
Từ (1), (2) suy ra: \(B C \perp(A M H)\).
Suy ra: \(\left\{\begin{array}{l}B C \perp A M \\ B C \perp M H\end{array} \Rightarrow[A, B C, D]=\widehat{A M H}\right.\).
Lại có: \(A H=\sqrt{A C^{2}-C H^{2}}=\sqrt{\left(\frac{a \sqrt{3}}{2}\right)^{2}-\left(\frac{a}{2}\right)^{2}}=\frac{a \sqrt{2}}{2}\).
\(\Rightarrow \tan \widehat{A M H}=\frac{A H}{M H}=\sqrt{3} \Rightarrow \widehat{A M H}=\frac{\pi}{3} \Rightarrow \cos \widehat{A M H}=\frac{1}{2}\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề Thi Tham Khảo Đánh Giá Năng Lực Năm 2024 – ĐHQG Hà Nội – Đề Số 01 là bài kiểm tra toàn diện và khoa học, giúp học sinh thể hiện năng lực giải quyết vấn đề, tư duy sáng tạo và phân tích logic. Với ba phần thi chính: Toán Học Và Xử Lí Số Liệu, Văn Học - Ngôn Ngữ, và Khoa Học/Tiếng Anh, đề thi không chỉ dừng lại ở việc kiểm tra kiến thức cơ bản mà còn yêu cầu thí sinh phát triển khả năng lập luận và ứng dụng thực tiễn. Đặc biệt, phần thi Khoa Học cho phép lựa chọn giữa Vật Lí, Hóa Học, Sinh Học, Lịch Sử, Địa Lí tạo điều kiện cho thí sinh phát huy thế mạnh cá nhân.
Câu hỏi liên quan
Ta có: \(1605632=2^{15}.7^{2}\)
Suy ra số các ước nguyên dương của 1605632 là \((15+1)(2+1)=48\).
Số phần tử của không gian mẫu: \(n(\Omega)=48\).
Trong đó, số các số chia hết cho 7 là: \((15+1) \cdot 2=32\).
Xác xuất cần tìm là: \(P=\frac{32}{48}=\frac{2}{3}\).
Ta có : \(2^{2 x-1}=8 \Leftrightarrow 2 x-1=3 \Leftrightarrow x=2\).
Ta có: \(\overrightarrow{n_{d_{1}}}=(4;-3); \overrightarrow{n_{d_{2}}}=(3; 4)\).
Do \(A\) không thuộc hai đường thẳng \(d_{1}; d_{2}\) và \(d_{1} \perp d_{2}\) nên độ dài hai cạnh kề nhau của hình chữ nhật bằng khoảng cách từ \(A\) đến hai đường thẳng \(d_{1}; d_{2}\).
Ta có:
\(d\left(A; d_{1}\right)=\frac{|4.2-3.1+5|}{\sqrt{4^{2}+3^{2}}}=2\).
\(d\left(A; d_{2}\right)=\frac{|3.2+4.1-5|}{\sqrt{3^{2}+4^{2}}}=1\).
\(\Rightarrow S=d\left(A; d_{1}\right). d\left(A; d_{2}\right)=2.1=2\).
Vận tốc tại thời điểm \(t\) là \(v(t)=s^{\prime}(t)=-\frac{3}{2} t^{2}+18 t\) với \(t \in[0; 10]\).
Ta có : \(v^{\prime}(t)=-3 t+18=0 \Leftrightarrow t=6\).
Suy ra: \(v(0)=0; v(10)=30; v(6)=54\).
Vậy vận tốc lớn nhất của vật đạt được bằng \(54~(\mathrm{m} / \mathrm{s})\).
Ta có: \(d:\left\{\begin{array}{l}x=2+t \\ y=1-3 t\end{array} \Rightarrow d: 3 x+y-7=0\right.\).
Để \(A, B\) nằm cùng phía đối với \(d\) thì:
\(\left(3 x_{A}+y_{A}-7\right)\left(3 x_{A}+y_{A}-7\right)>0 \Leftrightarrow-2(m-13)>0 \Leftrightarrow m-13<0 \Leftrightarrow m<13.\)
Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026
