Câu hỏi:
Tìm hệ số của \(x^{4}\) trong khai triển \(P(x)=\left(1-x-3 x^{3}\right)^{n}\) với \(n\) là số tự nhiên thỏa mãn hệ thức \(C_{n}^{n-2}+6 n+5=A_{n+1}^{2}\).
Đáp án đúng: C
Từ phương trình \(C_{n}^{n-2}+6 n+5=A_{n+1}^{2} \rightarrow n=10\).
Với \(n=10\), khi đó \(P(x)=\left(1-x-3 x^{3}\right)^{n}=\left(1-x-3 x^{3}\right)^{10}\).
Theo khai triển nhị thức Newton, ta có
\(P(x)=\left(1-x-3 x^{3}\right)^{10}=\left[1-\left(x+3 x^{3}\right)\right]^{10}=\sum_{k=0}^{10} C_{10}^{k}(-1)^{k}\left(x+3 x^{3}\right)^{k}\)
\(=\sum_{k=0}^{10} C_{10}^{k}(-1)^{k} x^{k}\left(1+3 x^{2}\right)^{k}=\sum_{k=0}^{10} C_{10}^{k} \sum_{l=0}^{k} C_{k}^{l}(-1)^{k} 3^{l} x^{k+2 l}\).
Số hạng chứa \(x^{4}\) trong khai triển tương ứng với \(\left\{\begin{array}{l}k+2 l=4 \\ 0 \leq k \leq 10 \\ 0 \leq l \leq k\end{array} \Leftrightarrow(k ; l)=\{(4 ; 0),(2 ; 1)\}\right.\).
Vậy hệ số của số hạng chứa \(x^{4}\) trong khai triển là \(C_{10}^{4} C_{4}^{0}+C_{10}^{2} C_{2}^{1} 3=480\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026

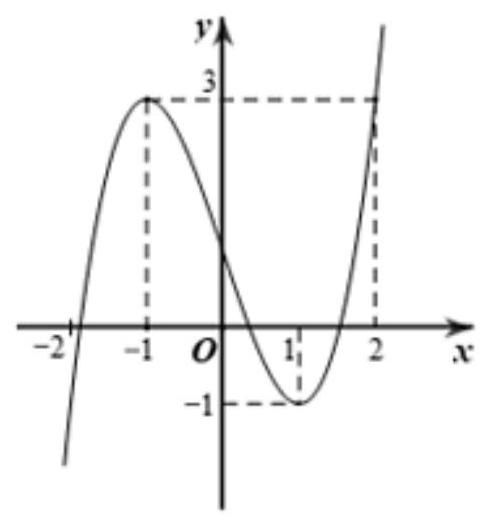 Xét hàm số \(g(x)=f\left(2 x^{3}+x-1\right)+m\). Với giá trị nào của \(m\) thì giá trị nhỏ nhất của \(g(x)\) trên đoạn \([0;1]\) bằng \(- 20\)
Xét hàm số \(g(x)=f\left(2 x^{3}+x-1\right)+m\). Với giá trị nào của \(m\) thì giá trị nhỏ nhất của \(g(x)\) trên đoạn \([0;1]\) bằng \(- 20\)