Câu hỏi:
Tổng các giá trị của tham số \(m\) để đường thẳng \(y=-x+2\) cắt đồ thị hàm số \(y=\frac{x^{3}+m}{x-1}\) tại hai điểm phân biệt bằng bao nhiêu?
Kết quả làm tròn đến chữ số thập phân thứ hai.
Đáp án đúng: -7,15
Phương trình hoành độ giao điểm của đường thẳng và đồ thị hàm số:
\(\frac{x^{3}+m}{x-1}=-x+2(x \neq 1) \Leftrightarrow-x^{3}-x^{2}+3 x-2=m(x \neq 1)(*)\).
Để đồ thị hàm số cắt đường thẳng tại hai điểm phân biệt thì phương trình (*) có hai nghiệm phân biệt khác 1.
Xét hàm số \(f(x)=-x^{3}-x^{2}+3 x-2\) trên \((-\infty ; 1) \cup(1 ;+\infty)\).
Ta có: \(f^{\prime}(x)=-3 x^{2}-2 x+3, f^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}x_{1}=\frac{-1-\sqrt{10}}{3} \\ x_{2}=\frac{-1+\sqrt{10}}{3}\end{array}\right.\).
Bảng biến thiên của hàm số \(f(x)\) :
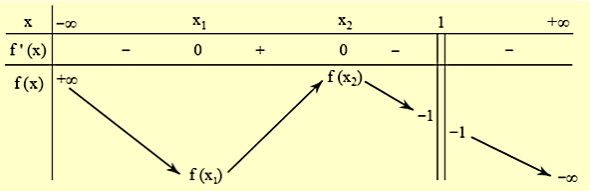
Từ bảng biến thiên ta có phương trình (*) có hai nghiệm phân biệt khác 1
\(\Leftrightarrow\left[\begin{array}{l}m=f\left(x_{1}\right) \\ m=f\left(x_{2}\right) \\ m=f(1)\end{array} \Leftrightarrow\left[\begin{array}{l}m=\frac{-83-20 \sqrt{10}}{27} \\ m=\frac{-83+20 \sqrt{10}}{27} \\ m=-1\end{array} \Rightarrow \sum m=-\frac{193}{27} \approx-7,15\right.\right.\)
Vậy tổng các giá trị của tham số \(m\) thỏa mãn là \(-7,15\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Câu hỏi liên quan
Gọi số cần tìm có dạng: \(\overline{a_{1} a_{2} a_{3} a_{4} a_{5} a_{6}}\) với \(a_{3}+a_{4}+a_{5}=8\)
Ta có: \(8=1+2+5=1+3+4(*)\).
Vậy có 2 cách chọn nhóm 3 số để các số hàng chục, hàng trăm, hàng nghìn có tổng bằng 8.
Bước 1: Chọn ra 3 trong 8 số thỏa mãn \(a_{3}+a_{4}+a_{5}=8\). Theo phân tích (*) có : 2 cách.
Bước 2: Với mỗi bộ ba số chọn ở bước 1 có: \(3!=6\) cách lập số \(\overline{a_{3} a_{4} a_{5}}\).
Bước 3: Chọn ra số \(\overline{a_{1} a_{2} a_{6}}\) theo thứ tự trên. Số cách chọn: \(A_{6}^{3}=120\).
Theo quy tắc nhân số cách chọn theo yêu cầu là: \(2 \cdot 6 \cdot 120\) =1440 số.
Gọi biến cố \(A\) : "lấy viên bi thứ nhất là màu xanh"; \(B\) : "lấy viên bi thứ hai là màu đỏ".
Ta có: \(P(A)=\frac{3.4}{5.4}=\frac{3}{5} ; P(A \cap B)=\frac{3.2}{5.4}=\frac{3}{10}\).
Do đó: \(P(B \mid A)=\frac{P(A \cap B)}{P(A)}=\frac{\frac{3}{10}}{\frac{3}{5}}=\frac{1}{2}\).
ТХĐ: \(D=[-2 ; 4]\).
Ta có: \(y^{\prime}=\frac{1-x}{\sqrt{8+2 x-x^{2}}} ; y^{\prime}=0 \Leftrightarrow x=1 \Rightarrow y(1)=3\)
Qua \(x=1, y^{\prime}\) đổi dấu từ dương sang âm nên cực đại của hàm số là 3.
Từ đồ thị hàm số \(y=f^{\prime}(x)\) và giả thiết \(f(-1)=\frac{13}{4}, f(2)=6\) ta có bảng biến thiên hàm số \(y=f(x)\) trên \([-1 ; 2]\):
Ta có \(g^{\prime}(x)=3 f^{2}(x) \cdot f^{\prime}(x)-3 f^{\prime}(x)\).
Xét trên đoạn \([-1 ; 2]: g^{\prime}(x)=0 \Leftrightarrow 3 f^{\prime}(x)\left[f^{2}(x)-1\right]=0\)
\(\Leftrightarrow f^{\prime}(x)=0\)
\(\Leftrightarrow\left[\begin{array}{l}x=-1 \\ x=2\end{array}\right.\)
Bảng biến thiên:
\(\Rightarrow \min _{[-1 ; 2]} g(x)=g(-1)=f^{3}(-1)-3 f(-1)=\frac{1573}{64}\).
Gọi \(A\) "Trong 5 phát biểu mời có đúng một phát biểu là của đại biểu nam".
Gọi \(B\) "Trong 5 phát biểu mời có đúng hai phát biểu là của đại biểu nam".
Suy ra \(A \cup B\) là "Trong 5 phát biểu mời có một hoặc hai phát biểu là của đại biểu nam".
Vì \(A\) và \(B\) là hai biến cố xung khắc nên \(P(A \cup B)=P(A)+P(B)\).
Ta có \(P(A)=\frac{C_{10}^{1} \cdot C_{20}^{4}}{C_{30}^{5}}, P(B)=\frac{C_{10}^{2} \cdot C_{20}^{3}}{C_{30}^{5}}\).
\(\Rightarrow P(A \cup B)=P(A)+P(B) \approx 0,7\)
Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026
