Trắc nghiệm Ứng dụng của tích phân trong hình học Toán Lớp 12
-
Câu 1:
Nam và Hùng tập sút phạt, ai sút trúng gôn nhiều hơn là người thẳng cuộc. Nếu để bóng ở vị trí A thì xác suất trúng vào gôn của Nam là 0,9 còn của Hùng là 0,7. Nếu để bóng ở vị trí B thì xác suất trúng vào gôn của Nam là 0,7 còn của Hùng là 0,8. Nam và Hùng đều đá một quả ở vị trí A và một quả ở vị trí B. Xác suất để Nam thắng cuộc là:
A. 0,2967.
B. 0,0378.
C. 0,2394.
D. 0,2976.
-
Câu 2:
Một vật có kích thước và hình dáng như hình vẽ dưới đây. Đáy là hình tròn giới hạn bởi đường tròn \(x^2+y^2=16\) (nằm trong mặt phẳng Oxy), cắt vật bởi các mặt phẳng vuông góc với trục Ox ta được thiết diện là hình vuông. Thể tích của vật thể là
.PNG)
A. \( V = \mathop \smallint \limits_{ - 4}^4 4\left( {16 - {x^2}} \right)dx\)
B. \( \mathop \smallint \limits_{ - 4}^4 4\pi {x^2}dx\)
C. \( \mathop \smallint \limits_{ - 4}^4 4 {x^2}dx\)
D. \( V = \mathop \smallint \limits_{ - 4}^4 4\pi \left( {16 - {x^2}} \right)dx\)
-
Câu 3:
Diện tích của hình phẳng giới hạn bởi các đường \( {y_1} = {x^3};{y_2} = 4x\) bằng
A. 0
B. 4
C. 8
D. -8
-
Câu 4:
Cho hình phẳng H giới hạn bởi các đường y=f(x),y=0, x=b và x=a (trong đó hàm số f(x) liên tục trên đoạn [b;a]). Thể tích khối tròn xoay tạo nên bởi phép quay hình H quanh trục Ox được cho bởi công thức:
A. \( \pi \mathop \smallint \limits_a^b {f^2}\left( x \right)dx\)
B. \( \mathop \smallint \limits_a^b {f^2}\left( x \right)dx\)
C. \( \pi \mathop \smallint \limits_b^a {f^2}\left( x \right)dx\)
D. \( \mathop \smallint \limits_a^b {\left[ {\pi f\left( x \right)} \right]^2}dx\)
-
Câu 5:
Quay hình phẳng Q giới hạn bởi các đường \( {y_2} = \frac{{2x}}{\pi };{y_1} = \sin x\) quanh trục Ox, ta được một khối tròn xoay. Khi đó thể tích của khối tròn xoay này bằng
A. \( \frac{1 }{6}\)
B. \( \frac{\pi }{6}\)
C. \(8\)
D. \( \frac{\pi^2 }{6}\)
-
Câu 6:
Quay hình phẳng G giới hạn bởi các đường y=x3,y=1,x=0 xung quanh trục Oy. Khi đó thể tích của khối tròn xoay này bằng:
A. \(\pi \)
B. \( \frac{5}{3}\pi \)
C. \( \frac{3}{5}\pi \)
D. \( \frac{3}{5}\)
-
Câu 7:
Quay hình phẳng Q giới hạn bởi các đường y1=sinx và \( {y_2} = \frac{{2x}}{\pi }\) quanh trục Ox, ta được một khối tròn xoay. Khi đó thể tích của khối tròn xoay này bằng
A. \( \frac{{1}}{6}\)
B. \( \frac{{{\pi}}}{6}\)
C. \(6\)
D. \( \frac{{{\pi ^2}}}{6}\)
-
Câu 8:
Quay hình phẳng GG giới hạn bởi các đường y=x3,y=1,x=0 xung quanh trục Oy. Khi đó thể tích của khối tròn xoay này bằng
A. \(5\pi \)
B. \( \frac{1}{5}\pi \)
C. \( \frac{3}{5}\pi \)
D. \(3\pi \)
-
Câu 9:
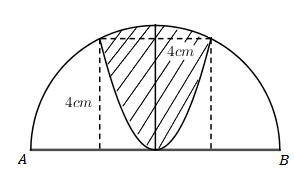
Cho nửa đường tròn đường kính (\(AB=4\sqrt5\) ). Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hai điểm cách nhau 4cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần gạch chéo trong hình vẽ). Đem phần còn lại quay xung quanh trục AB. Thể tích của khối tròn xoay thu được bằng:
A. \( V = \frac{\pi }{5}\left( {800\sqrt 5 - 928} \right){\mkern 1mu} c{m^3}\)
B. \( V = \frac{\pi }{{15}}\left( {800\sqrt 5 - 928} \right)c{m^3}\)
C. \( V = \frac{\pi }{{3}}\left( {800\sqrt 5 - 928} \right)c{m^3}\)
D. \( V = \frac{\pi }{{15}}\left( {800\sqrt 5 - 464} \right)c{m^3}\)
-
Câu 10:
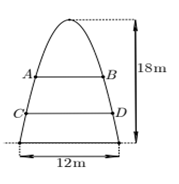
Một cổng chào có dạng hình parabol chiều cao 18m, chiều rộng chân đế 12m. Người ta căng sợi dây trang trí AB, CD nằm ngang đồng thời chia hình giới hạn bởi parabol thành ba phần có diện tích bằng nhau (xem hình vẽ bên). Tỉ số \( \frac{{AB}}{{CD}}\)
A. \( \frac{1}{{\sqrt 2 }}\)
B. \( \frac{4}{5}\)
C. \( \frac{1}{{\sqrt[3]{2}}}\)
D. \( \frac{3}{{1 + 2\sqrt 2 }}\)
-
Câu 11:
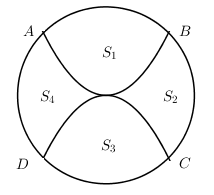
Sân trường THPT Chuyên Hà Giang có một bồn hoa hình tròn có tâm O. Một nhóm học sinh lớp 12 được giao thiết kế bồn hoa, nhóm này chia bồn hoa thành bốn phần, bởi hai đường Parabol có cùng đỉnh O và đối xứng nhau qua O. Hai đường Parabol này cắt đường tròn tại bốn điểm A, B, C, D tạo thành một hình vuông có cạnh bằng 4m (như hình vẽ). Phần diện tích (S1,S3 ) dùng để trồng hoa, phần diện tích (S2,S4 ) dùng để trồng cỏ (Diện tích được làm tròn đến hàng phần trăm). Biết kinh phí trồng hoa là (150.000 ) đồng/ (m2 ), kinh phí trồng cỏ là (100.000 ) đồng/ (m2 ). Hỏi cả trường cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm tròn đến hàng chục nghìn).
A. 3.000.000 đồng
B. 6.060.000 đồng
C. 3.270.000 đồng
D. 5.790.000 đồng
-
Câu 12:
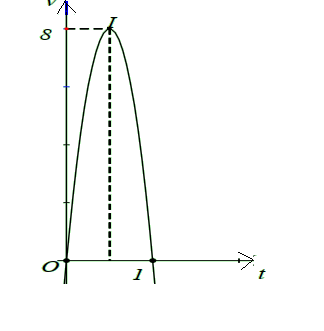
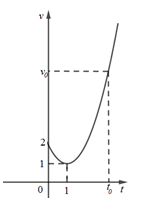
Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ thuộc vào thời gian t ,(h) có đồ thị là một phần của đường parabol có đỉnh I(1;1) và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s mà vật di chuyển được trong 4 giờ kể từ lúc xuất phát
A. \( s =6(km).\)
B. \( s = 8(km).\)
C. \( s = \frac{{46}}{3}(km).\)
D. \( s = \frac{{40}}{3}(km).\)
-
Câu 13:
Cho miền phẳng \(\left( D \right)\) giới hạn bởi \(y = \sqrt x \), hai đường thẳng x = 1, x = 2 và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay \(\left( D \right)\) quanh trục hoành.
A. \(3\pi\)
B. \(\frac{{3\pi }}{2}\)
C. \(\frac{{2\pi }}{3}\)
D. \(\frac{3}{2}\)
-
Câu 14:
Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v(t)=\frac{1}{120} t^{2}+\frac{58}{45} t(\mathrm{~m} / \mathrm{s})\) , trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 3 giây so với A và có gia tốc bằng \(a\left(\mathrm{~m} / \mathrm{s}^{2}\right)\) (a là hằng số). Sau khi B xuất phát được 15 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kip A bằn
A. 10m/s
B. 20m/s
C. 30m/s
D. 40m/s
-
Câu 15:
Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theothời gian bởi quy luật \(v(t)=\frac{1}{100} t^{2}+\frac{13}{30} t(\mathrm{~m} / \mathrm{s})\), trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 10 giây so với A và có gia tốc bằng \(a\left(\mathrm{~m} / \mathrm{s}^{2}\right)\) (a là hằng số). Sau khi B xuất phát được 15 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kip A bằng:
A. 10m/s
B. 15m/s
C. 20m/s
D. 25m/s
-
Câu 16:
Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v(t)=\frac{1}{150} t^{2}+\frac{59}{75} t(\mathrm{~m} / \mathrm{s})\) trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 3 giây so với A và có gia tốc bằng \(a\left(\mathrm{~m} / \mathrm{s}^{2}\right)\) (a là hằng số). Sau khi B xuất phát được 12 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kip A bằng:
A. 12m/s
B. 16m/s
C. 20m/s
D. 24m/s
-
Câu 17:
Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v(t)=\frac{1}{180} t^{2}+\frac{11}{18} t(\mathrm{~m} / \mathrm{s})\), trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 5 giây so với A và có gia tốc bằng \(a\left(\mathrm{~m} / \mathrm{s}^{2}\right)\) (a là hằng số). Sau khi B xuất phát được 10 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kip A bằn
A. 22m/s
B. 15m/s
C. 30m/s
D. 11m/s
-
Câu 18:
Một xe lửa chuyển động chậm dần đều và dừng hẳn sau 20 giây kể từ khi bắt đầu hãm phanh. Trong thời gian đó xe chạy được 120m . Cho biết công thức vận tốc của chuyển động biến đổi đều là \(v(t)=v_{0}+a t(\mathrm{~m} / \mathrm{s})\) , trong đó \(a\left(\mathrm{~m} / \mathrm{s}^{2}\right)\) là gia tốc và v(m/s) là vận tốc tại thời điểm t(s ) . Hãy tính vận tốc v0 lúc bắt đầu hãm phanh
A. 12m/s
B. 6m/s
C. 30m/s
D. 15m/s
-
Câu 19:
Một ô tô bắt đầu chuyển động nhanh dần đều với gia tốc \(a_{1}=7\left(m / s^{2}\right)\). Đi được 5s , tài xế phát hiện chướng ngại vật phía trước và phanh gấp, sáu đó ô tô chuyển động chậm dần đều với gia tốc \(a_{2}=-70\left(\mathrm{~m} / \mathrm{s}^{2}\right) \text { . }\)Tính quãng đường đi được của ô tô từ lúc bắt đầu chuyển động cho đến khi dừng hẳn.
A. 87,5m .
B. 96, 25m.
C. 94m
D. 95,7m
-
Câu 20:
Một tập đoàn định đầu tư vào hai dự án. Giả sử, dự án đầu tư đầu có tốc độ sinh lợi nhuận là \(P_{1}(t)=50+t^{2}(\text { đồng/năm) }\), dự án thứ hai có tốc độ sinh lợi nhuận là \(P_{2}(t)=200+5 t(\text { đồng/năm) }\). Sau t năm thì tốc độ sinh lợi của dự án hai bằng một nửa dự án một. Tính lợi nhuận thực tế trong khoảng thời gian trên.
A. \(\begin{array}{llll} 6674,6 \text { đồng. } \end{array}\)
B. \( 6576,4 \text { đồng. }\)
C. \(5676,4 \text { đồng. } \)
D. \(6679,4 \text { đồng. }\)
-
Câu 21:
Một nhóm sinh viên được thực hành nghiên cứu sự chuyển động của các hạt. Nhóm đã phát hiện hạt prô-ton di chuyển trong điện trường với gia rốc \(a=-\frac{20}{(1+2 t)^{2}}\left(\mathrm{~cm} / \mathrm{s}^{2}\right)\) . Nhóm sinh viên đã tìm ra hàm vận tốc của hạt đó, biết khi t = 0 thì vận tốc là \(v=30 \mathrm{~cm} / \mathrm{s}\) . Biểu thức đúng là?
A. \(\begin{array}{l} v(t)=\left(\frac{10}{1+2 t}+25\right) \mathrm{cm} / \mathrm{s} . \end{array}\)
B. \( v(t)=\left(\frac{10}{1+2 t}+20\right) \mathrm{cm} / \mathrm{s} .\)
C. \(v(t)=\left(\frac{10}{1+2 t}+10\right) \mathrm{cm} / \mathrm{s} .\)
D. \(v(t)=\left(\frac{10}{1+2 t}+30\right) \mathrm{cm} / \mathrm{s} \text { . }\)
-
Câu 22:
Con cá bơi có phương trình quãng đường \(s(t)=-\frac{1}{10} t^{2}+4 t(\mathrm{~km})\), t tính bằng giờ. Biết con cá bơi xuôi dòng nước với tốc độ dòng chảy là 2 / km h . Tính khoảng cách xa nhất con cá bơi được?
A. 10km
B. 40km
C. 60km
D. 90km
-
Câu 23:
Một vật chuyển động với vận tốc đấu là v( ) 0 ( ) m s / và có gia tốc được cho bởi công thức \(a(t)=v^{\prime}(t)=\frac{2}{t+1}\left(m / s^{2}\right)\). Vận tốc của vật sau 15 giây là \(v(15)=8 \ln 2-\log 100(m / s)\) . Tính vận tốc ban đầu của vật.
A. 9m/s
B. 10m/s
C. 11m/s
D. 12m/s
-
Câu 24:
Một vật bắt đầu chuyển động với vận tốc đầu là 6(m/s) và có gia tốc được cho bởi công thức \(a(t)=v^{\prime}(t)=\frac{3}{t+1}\left(m / s^{2}\right) .\) Vận tốc của vật sau 8 giây là \(v(8)=a \ln 3+b(a, b \in \mathbb{Z}), \text { tính } P=a-b \text { . }\)
A. 1
B. -1
C. 0
D. 2
-
Câu 25:
Một vật bắt đầu chuyển động với vận tốc thay đổi theo thời gian được tính bởi công thức \(v(t)=3 t+2(m / s)\) . Tại thời điểm t = 2s thì vật đã đi được quãng đường là 10m. Hỏi tại thời điểm t = 30s thì vật đã đi quãng đường bao nhiêu m từ lúc bắt đầu chuyển động?
A. 1140m
B. 1410m
C. 400m
D. 401m
-
Câu 26:
Bạn Minh ngồi trên một máy bay đi du lịch thế giới với vận tốc chuyển động của máy bay là \(v(t)=3 t^{2}+5(m / s)\). Quãng đường máy bay đi được từ giây thứ thứ 5 đến giây thứ 10 là
A. 900m
B. 936m
C. 1134m
D. 966m
-
Câu 27:
Một chiếc máy bay chuyển động trên đường băng với vận tốc \(v(t)=t^{2}+10 t(m / s),\) với t là thời gian được tính theo đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận tốc 200 (m/s) thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là:
A. \(\frac{2500}{3} m\)
B. 2000 m
C. 500 m
D. \(\frac{4000}{3} m .\)
-
Câu 28:
Một vật bắt đầu chuyển động với phương trình vận tốc là \(v(t)=\frac{2 t}{t^{2}+1}\).Hỏi từ lúc bắt đầu chuyển động đến khi vật có tốc độ lớn nhất đã đi được quãng đường dài bao nhiêu?
A. ln2 (m)
B. log2 (m)
C. 1(m)
D. ln4 (m)
-
Câu 29:
Một vật bắt đầu chuyển động với phương trình vận tốc là \(v(t)=\frac{2 t}{t^{2}+1}\) Hỏi từ lúc bắt đầu chuyển động đến khi vật có gia tốc nhỏ nhất đã đi được quãng đường dài bao nhiêu?
A. ln2 (m)
B. log 2 (m)
C. log4 (m)
D. ln4 (m)
-
Câu 30:
Một vật chuyển động với phương trình vận tốc là \(v(t)=t^{3}-9 t^{2}+24 t-16(\mathrm{~m} / \mathrm{s})\) . Hỏi từ lúc t = 0 đến khi vật có gia tốc nhỏ nhất thì vật đã đi được quãng đường bao nhiêu?
A. 12,75m
B. 13m
C. 1m
D. 0,75m
-
Câu 31:
Một vật bắt đầu chuyển động \(v(t)=2 t^{3}-15 t^{2}+24 t+20(\mathrm{~m} / \mathrm{s})\) . Hỏi trong 5 giây đầu tiên, quãng đường vật đi được cho đến khi đạt vận tốc lớn nhất là bao nhiêu?
A. 132m
B. \(\frac{175}{2} \mathrm{~m}\)
C. 81m
D. \(\frac{55}{2} \mathrm{~m}\)
-
Câu 32:
Một vật chuyển động chậm dần đều với vận tốc \(v(t)=160-10 t(\mathrm{~m} / \mathrm{s})\) . Quãng đường vật đi được từ lúc t = 0 đến thời điểm mà vật dừng lại là
A. 160m .
B. 100m
C. 1280m
D. 144m
-
Câu 33:
Một vật chuyển động với vận tốc 10 (m/s) thì tăng tốc với gia tốc \(a(t)=3 t+t^{2}\left(\mathrm{~m} / \mathrm{s}^{2}\right)\) Quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc là
A. \(\frac{400}{3} \mathrm{~m} . \)
B. \(\frac{430}{3} \mathrm{~m} \cdot\)
C. \( \frac{4300}{3} \mathrm{~m} . \)
D. \( \frac{4000}{3} \mathrm{~m} .\)
-
Câu 34:
Một vật chuyển động với vận tốc \(v(t)=1-2 \sin 2 t(m / s) . \text { Gọi } S=a+\frac{b \pi}{c}(a, b, c \in \mathbb{Z}, \frac{b}{c}\) tối giản) là quảng đường vật di chuyển trong khoảng thời gian từ thời điểm t=0(s) đến thời điểm \(t=\frac{3 \pi}{4} . \text { Tính } P=2 a-3 b+2 c .\)
A. P=-1
B. P=1
C. P=-3
D. P=3
-
Câu 35:
Một vật từ trạng thái nghỉ t=0(s) chuyển động thẳng với vân tốc \(v(t)=t(6-t)(m / s)\) . Tính quãng đường vật đi được cho đến khi nó dừng lại.
A. 20
B. 26
C. 30
D. 36
-
Câu 36:
Cá hồi Thái Bình Dương đến mùa sinh sản chúng thường bơi từ biển đến thượng nguồn con sông để đẻ trứng trên sỏi đá rồi chết. Khi nghiên cứu một con cá hồi sinh sản người ta phát hiện ra một quy luật nó chuyển động trong nước yên lặng là \(s(t)=-\frac{t^{2}}{10}+4 t\) với t (giờ) là khoảng thời gian từ lúc con cá bắt đầu chuyển động và s(t) ( km ) là quãng đường con cá bơi trong khoảng thời gian đó. Nếu thả con cá hồi vào dòng sông có vận tốc dòng nước chảy là 2 km/h. Tính khoảng cách xa nhất mà con cá hồi đó có thể bơi ngược dòng nước đến nơi để trứng
A. 8km
B. 10km
C. 20km
D. 40km
-
Câu 37:
Một chất điểm A xuất phát từ vị trí O, chuyển động thẳng nhanh dần đều; 8 giây sau nó đạt vận tốc 6 m/s . Từ thời điểm đó nó chuyển động thẳng đều. Một chất điểm B cũng xuất phát từ cùng vị trí O nhưng chậm hơn 12 giây so với A và chuyển động nhanh dần đều. Biết rằng B đuổi kịp A sau 8 giây (kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đuổi kịp A .
A. \(24 \mathrm{~m} / \mathrm{s} .\)
B. \(12 \mathrm{~m} / \mathrm{s}\)
C. \(48 \mathrm{~m} / \mathrm{s}\)
D. \(36 \mathrm{~m} / \mathrm{s}\)
-
Câu 38:
Một ô tô đang chạy với vận tốc 18 (m/s) thì người lái hãm phang. Sau khi hãm phanh ô tô chuyển động chậm dẫn đều với vận tốc \(v(t)=18-36 t(\mathrm{~m} / \mathrm{s})\) , trong đó t là khoảng thời gian được tính bằng giây kể từ lúc ô tô bắt đầu hãm phanh. Tính quãng đường ô tô đi được kể từ lúc hãm phang cho đến khi dừng hẳn.
A. 3,5m
B. 4,5m
C. 5,5m
D. 6,5m
-
Câu 39:
Một vật đang chuyển động đều với vận tốc \(v_{0}=15 \mathrm{~m} / \mathrm{s}\) thì tăng tốc với gia tốc \(a(t)=t^{2}+4 t\left(m / s^{2}\right)\). Tính quãng đường vật đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng tốc.
A. 27m .
B. 72m
C. 69,75m.
D. 24,75m .
-
Câu 40:
Giả sử một vật từ trạng thái nghỉ t=0(s) chuyển động thẳng với vận tốc \(v_{t}=t(5-t)(\mathrm{m} / \mathrm{s})\) . Tính quãng đường vật đi được cho tới khi nó dừng lại.
A. \(\frac{125}{6}(m) .\)
B. 25m
C. 12m
D. 31m
-
Câu 41:
Một vật đang chuyển động đều với vận tốc \(v_{0}(m / s)\) thì bắt đầu tăng tốc với gia tốc \(a(t)=v_{0} t+t^{2}\left(m / s^{2}\right)\) trong đó t là khoảng thời gian được tính bằng giây kể từ thời điểm vật bắt đầu tăng tốc. Biết quãng đường vật đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng tốc là 100m. Tính vận tốc ban đầu v0 của vật.
A. \(20,722(\mathrm{~m} / \mathrm{s}) .\)
B. \(\begin{array}{l} 12,433(\mathrm{~m} / \mathrm{s}) . \end{array}\)
C. \(21,722(\mathrm{~m} / \mathrm{s}) .\)
D. \(13,433(\mathrm{~m} / \mathrm{s}) \text { . }\)
-
Câu 42:
Để đảm bảo an toàn khi lưu thông trên đường, các xe ô tô khi dừng đèn đỏ phải cách nhau tối thiểu 1m . Ô tô A đang chạy với vận tốc 16m/s bỗng gặp ô tô B đang dừng đèn đỏ nên ô tô A chuyển động chậm dần đều với vận tốc \(v(t)=16-4 t(m / s)\), trong đó t là khoảng thời gian tính bằng giây kể từ thời điểm ô tô A bắt đầu hãm phanh. Hỏi rằng để hai ô tô A và B dừng lại đạt khoảng cách an toàn thì ô tô A phải hãm phanh khi cách ô tô B một khoảng tối thiểu là bao nhiêu mét?
A. 31m
B. 32m
C. 33m
D. 34m
-
Câu 43:
Tại một noiw không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật \(v(t)=10 t-t^{2}\), trong đó t ( phút) là thời gian tính từ lúc bắt đầu chuyển động, v(t) được tính theo đơn vị mét/phút (m/p). Nếu như vậy thì bắt đầu tiếp đất vận tốc v của khí cầu là?
A. \(v=5(m / p)\)
B. \(v=7(m / p)\)
C. \(v=3(m / p)\)
D. \(v=9(m / p)\)
-
Câu 44:
Cho đồ thị biểu thị vận tốc của hai xe A và B khởi hành cùng một lúc, bên cạnh nhau và trên cùng một con đường. Biết đồ thị biểu diễn vận tốc của xe A là một đường Parabol, đồ thị biểu diễn vận tốc của xe B là một đường thẳng ở hình bên. Hỏi sau khi đi được 3 giây, khoảng cách giữa hai xe là bao nhiêu mét?
.PNG)
A. 90m
B. 60m
C. 0m
D. 270m
-
Câu 45:
Một người chạy trong 1 giờ với vận tốc v(km/h) phụ thuộc thời gian t (h) có đồ thị của vận tốc là một phần của đường parabol có đỉnh \(I\left(\frac{1}{2} ; 8\right)\) và trục đối xứng song song với trục tung như hình vẽ bên. Tính quãng đường s mà người đó chạy được trong khoảng thời gian 45 phút, kể từ khi bắt đầu chạy
A. \(s=4(\mathrm{~km}) .\)
B. \(s=2,3(\mathrm{~km}) . \)
C. \(s=4,5(\mathrm{~km})\)
D. \(s=5,3(\mathrm{~km})\)
-
Câu 46:
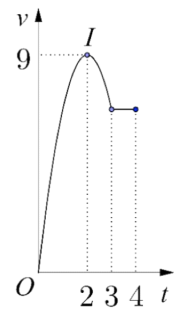
Một vật chuyển động trong 4 giờ với vận tốc v(km/h) phụ thuộc thời gian t(h ) có đồ thị của vận tốc như hình vẽ bên. Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh I ( 2;9) và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường s mà vật di chuyển được trong 4 giờ đó.
A. \(s=26,25(\mathrm{~km}) .\)
B. \(s=28,5(\mathrm{~km}) \cdot\)
C. \( s=27(\mathrm{~km}) \)
D. \(s=24(\mathrm{~km})\)
-
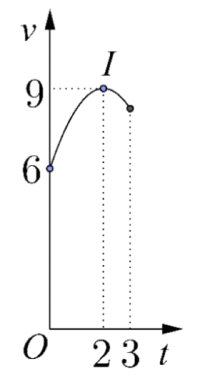
Câu 47:
Một vật chuyển động trong 3 giờ với vận tốc v(km/h) phụ thuộc thời gian t(h) có đồ thị của vận tốc là một phần của đường parabol có đỉnh I (2;9) và trục đối xứng song song với trục tung như hình vẽ. Tính quãng đường s mà vật di chuyển được trong 3 giờ đó
A. \(s=24,25(\mathrm{~km}) . \)
B. \(s=26,75(\mathrm{~km}) .\)
C. \(s=24,75(\mathrm{~km}) .\)
D. \(s=25,25(\mathrm{~km}) .\)
-
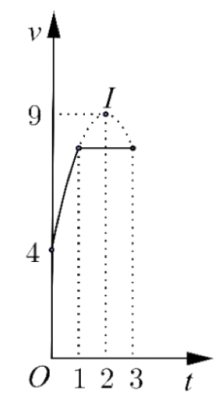
Câu 48:
Một vật chuyển động trong 3 giờ với vận tốc v(km/h) phụ thuộc thời gian t (h) có đồ thị của vận tốc như hình vẽ bên. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh I (2;9) và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường s mà vật di chuyển được trong 3 giờ đó (kết quả làm tròn hàng phần trăm):
A. \(s=23,25(\mathrm{~km})\)
B. \(s=21,58(\mathrm{~km})\)
C. \(s=15,50(\mathrm{~km})\)
D. \(s=13,83(\mathrm{~km})\)
-
Câu 49:
Cho hình phẳng B giới hạn bởi các đường \(x = \sqrt {2\sin 2y} ,x = 0,y = 0\) và \(y = {\pi \over 2}.\)
Tính thể tích của khối tròn xoay tạo thành khi quay hình B quanh trục tung.A. \( \pi \)
B. \( 2\pi \)
C. \( 3\pi \)
D. \( 4\pi \)
-
Câu 50:
Cho hình phẳng A giới hạn bởi các đường \(y = x{e^{{x \over 2}}},y = 0,x = 0\) và \(x = 1\).
Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.A. \(V = \pi \left( {e + 2} \right).\)
B. \(V = \pi \left( {e -1} \right).\)
C. \(V = \pi \left( {e - 2} \right).\)
D. \(V = \pi \left( {e - 3} \right).\)
