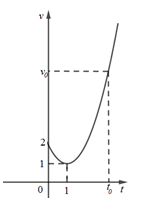
Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ thuộc vào thời gian t ,(h) có đồ thị là một phần của đường parabol có đỉnh I(1;1) và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s mà vật di chuyển được trong 4 giờ kể từ lúc xuất phát

Tính thể tích vật thể có đáy là một tam giác cho bởi: \(\displaystyle  y = x,y = 0\), và \(\displaystyle  x = 1\). Mỗi thiết diện vuông góc với trục \(\displaystyle  Ox\) là một hình vuông.

Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = {x^4} - 4{x^2} + 4,y = {x^2}\), trục tung và đường thẳng \(x = 1\)

Diện tích của hình phẳng giới hạn bởi các đường \(y = x^2+ 1 , y = 0, x = - 1, x = 2 \) bằng:

Hình phẳng giới hạn bởi đồ thị hàm số \(y=x^{3}\) , trục Ox và đường thẳng x =-2 có diện tích là

Tính thể tích khối tròn xoay khi quay hình phẳng xác định bởi: \(\displaystyle  y = {(2x + 1)^{\frac{1}{3}}},x = 0,y = 3\), quanh trục \(\displaystyle  Oy\).

Tính thể tích của một vật thể tròn xoay được tạo bởi một hình phẳng giới hạn bởi các đường: \(y = {x^2} - 4;y = 2x - 4;x = 0;x = 2\) và quay quanh trục Ox.

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {\cos ^2}x,\) trục hoành, trục tung và đường thẳng \(x = \pi \)

Quay hình phẳng ( H) như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn xoay có thể tích là

Cho hình phẳng H giới hạn bởi các đường y=f(x),y=0, x=b và x=a (trong đó hàm số f(x) liên tục trên đoạn [b;a]). Thể tích khối tròn xoay tạo nên bởi phép quay hình H quanh trục Ox được cho bởi công thức:

Diện tích hình phẳng giới hạn bởi các đường \(y=\left|x^{2}-4 x+3\right|, y=x+3 \text { là } S=\frac{a}{b}, (a ; b \in \mathbb{Z} ; a \neq 0) ; \frac{a}{b}\) là phân số tối giản. Khẳng định nào sau đây là đúng?

Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = a, x = b (a < b) quanh trục Ox.

Ông An có một mảnh vườn hình elip có độ dài trục lớn bằng 16m và độ dài trục bé bằng 10m . Ông muốn trồng hoa trên một dải đất rộng 8m và nhận trục bé của elip làm trục đối xứng (như hình vẽ). Biết kinh phí để trồng hoa là 100.000 đồng/1m2 . Hỏi ông An cần bao nhiêu tiền để trồng hoa trên dải đất đó? (Số tiền được làm tròn đến hàng nghìn).

Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường \(y=\sqrt{x+1}\) và trục Ox quay quanh trục Ox biết đáy lọ và miệng lọ có đường kính lần lượt là 2dm và 4dm, khi đó thể tích của lọ là:

Cho hình phẳng A giới hạn bởi các đường \(y = x{e^{{x \over 2}}},y = 0,x = 0\) và \(x = 1\).
Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.

Tính diện tích hình phẳng giới hạn bởi các đường có phương trình \(x = {y^3}\), \(y = 1\), và \(x = 8\).

Quay hình phẳng \(\displaystyle  Q\) giới hạn bởi các đường \(\displaystyle  {y_1} = \sin x\) và \(\displaystyle  {y_2} = \frac{{2x}}{\pi }\) quanh trục \(\displaystyle  Ox\), ta được một khối tròn xoay. Khi đó thể tích của khối tròn xoay này bằng

Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi đường elip ( E) : \(x^{2}+9 y^{2}=9\) quay quanh Ox bằng

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^3} - 3{x^2} + 2x\), trục hoành, trục tung và đường thẳng \(x = 3\)

Thể tích khối tròn xoay tạo bởi phép quay quanh trục \(\displaystyle  Ox\) của hình phẳng giới hạn bởi các đường \(\displaystyle  y = {\sin ^{\frac{3}{2}}}x,y = 0,x = 0\) và \(\displaystyle  x = \frac{\pi }{2}\) bằng

Cho hình phẳng B giới hạn bởi các đường \(x = \sqrt 5 {y^2},x = 0,y =  - 1\) và \(y = 1\). Tính thể tích của khối tròn xoay tạo thành khi quay hình B quanh trục tung.