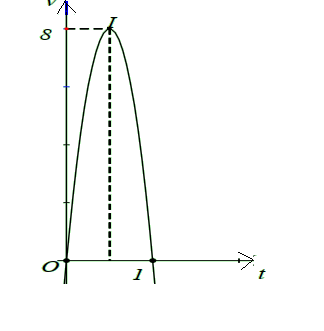
Một người chạy trong 1 giờ với vận tốc v(km/h) phụ thuộc thời gian t (h) có đồ thị của vận tốc là một phần của đường parabol có đỉnh \(I\left(\frac{1}{2} ; 8\right)\) và trục đối xứng song song với trục tung như hình vẽ bên. Tính quãng đường s mà người đó chạy được trong khoảng thời gian 45 phút, kể từ khi bắt đầu chạy 

Một vật chuyển động với phương trình vận tốc là \(v(t)=t^{3}-9 t^{2}+24 t-16(\mathrm{~m} / \mathrm{s})\) . Hỏi từ lúc t = 0 đến khi vật có gia tốc nhỏ nhất thì vật đã đi được quãng đường bao nhiêu? 

Diện tích hình phẳng giới hạn bởi hai đường thẳng \(x=0 , x=\pi \) đồ thị hàm số y=cos x và trục Ox là

Tính thể tích khối tròn xoay khi quay hình phẳng xác định bởi: \(\displaystyle  y = 2 - {x^2},y = 1\), quanh trục \(\displaystyle  Ox\).

Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường \(y=\sqrt{x+1}\) và trục Ox quay quanh trục Ox biết đáy lọ và miệng lọ có đường kính lần lượt là 2dm và 4dm, khi đó thể tích của lọ là:

Cho hình phẳng (H) giới hạn bởi đồ thị hàm số \(y=\frac{1}{x}\), trục Ox và hai đường thẳng \(x=1, x=2\). Khối tròn xoay tạo thành khi quay hình phẳng (H) quanh trục Ox có thể tích là

Quay hình phẳng Q giới hạn bởi các đường \( {y_2} = \frac{{2x}}{\pi };{y_1} = \sin x\) quanh trục Ox, ta được một khối tròn xoay. Khi đó thể tích của khối tròn xoay này bằng

Tại một noiw không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật \(v(t)=10 t-t^{2}\), trong đó t ( phút) là thời gian tính từ lúc bắt đầu chuyển động, v(t) được  tính theo đơn vị mét/phút (m/p). Nếu như vậy thì bắt đầu tiếp đất vận tốc v của khí cầu là?
 

Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y=f(x)=x^{4}-2 x^{2}\)2 và
trục hoành như hình vẽ bên. Khẳng định nào sau đây sai?

Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng xác định bởi \(\displaystyle  y = {x^{\frac{2}{3}}},x = 0\) và tiếp tuyến với đường \(\displaystyle  y = {x^{\frac{2}{3}}}\) tại điểm có hoành độ \(\displaystyle  x = 1\), quanh trục \(\displaystyle  Oy\)

Trên mặt phẳng Oxy, cho hình phẳng ( ) H giới hạn bởi các đường \(\begin{aligned} &(P): y=x^{2},\left(P^{\prime}\right): y=4 x^{2} \text { và } \text { (d): } y=4 \end{aligned}\) . Thể tích của khối tròn xoay khi quay (H ) quanh trục
Ox bằng

Tính diện tích hình phẳng giới hạn bởi các đường sau: \(\displaystyle  y = {x^3} - 1\) và tiếp tuyến với \(\displaystyle  y = {x^3} - 1\) tại điểm \(\displaystyle  \left( { - 1; - 2} \right)\).

Cho hàm số y=f(x) liên tục trên [ a;b ]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng (x=a; x=b) được tính theo công thức

Diện tích hình phẳng giới hạn bởi các đường \(y=x^{2}-2 x+1, y=x+1, x=0, x=m,(0<m<3)\) bằng:

Thể tích của khối tròn xoay khi quay hình phẳng D giới hạn bởi các đường \(y=\sqrt{x}\) và y=x quanh trục Ox bằng

Cho hình H giới hạn bởi đường cong y² + x = 0, trục Oy và hai đường thẳng y = 0,y = 1. Thể tích khối tròn xoay tạo thành khi quay H  quanh trục Oy )được tính bởi:

Gọi D là hình phẳng giới hạn bởi các đường y = 2^x, y = 0, x = 0 và x = 2.Thể tích V của khối tròn xoay tạo thành khi quay D quanh trục Ox )được xác định bởi công thức:

Tính thể tích của một vật thể tròn xoay được tạo bởi một hình phẳng giới hạn bởi các đường: \(y = \ln x;x = 0;y = 0;y = 1\) và quay quanh trục Oy.

Diện tích của hình phẳng được giới hạn bởi các đường \(\displaystyle  y = \tan x,y = 0,x =  - \frac{\pi }{4}\) và \(\displaystyle  x = \frac{\pi }{4}\) bằng

Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng xác định bởi \(\displaystyle  y = \left| {2x - {x^2}} \right|,y = 0\) và \(\displaystyle  x = 3\), quanh trục Ox.

Quay hình phẳng GG giới hạn bởi các đường y=x³,y=1,x=0 xung quanh trục Oy. Khi đó thể tích của khối tròn xoay này bằng