Trắc nghiệm Ứng dụng của tích phân trong hình học Toán Lớp 12
-
Câu 1:
Thể tích vật thể tròn xoay sinh ra khi quay hình phẳng giới hạn bới các đường \(x=\sqrt y; ,y=-x+2,x=0 \) quanh trục Ox có giá trị là kết quả nào sau đây ?
A. \( V = \frac{2}{3}\pi \)
B. \( V = \frac{1}{3}\pi \)
C. \( V = \frac{11}{6}\pi \)
D. \( V = \frac{32}{15}\pi \)
-
Câu 2:
Cho hình H giới hạn bởi đường cong y2 + x = 0, trục Oy và hai đường thẳng y = 0,y = 1. Thể tích khối tròn xoay tạo thành khi quay H quanh trục Oy )được tính bởi:
A. \(V = {\pi ^2}\mathop \smallint \limits_0^1 {x^4}d\)
B. \( V = \pi \mathop \smallint \limits_0^1 {y^2}dy\)
C. \(V = \pi \mathop \smallint \limits_0^1 {y^4}d\)
D. \( V = \pi \mathop \smallint \limits_0^1 - {y^4}dy\)
-
Câu 3:
Cho hình (H) giới hạn bởi đường cong \(x = \sqrt y \), trục tung và hai đường thẳng y = 1,y = 4 Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Oy được tính theo công thức
A. \( V = \pi \mathop \smallint \limits_1^4 \left| {\sqrt y } \right|dy\)
B. \(V = \mathop \smallint \limits_1^4 {y^2}dy\)
C. \( V = \pi \mathop \smallint \limits_1^4 {y^2}dy\)
D. \( V = \pi \mathop \smallint \limits_1^4 ydy\)
-
Câu 4:
Cho hình H giới hạn bởi đồ thị hàm số x = f(y) , trục tung và hai đường thẳng y = a,y = b. Thể tích khối tròn xoay tạo thành khi quay H quanh trục Oy là:
A. \( V = \pi \mathop \smallint \limits_a^b \left| {f\left( y \right)} \right|dy\)
B. \( V = \mathop \smallint \limits_a^b \left| {f\left( x \right)} \right|dx\)
C. \(V= {\pi ^2}\mathop \smallint \limits_a^b {f^2}\left( x \right)dx\)
D. \( V = \pi \mathop \smallint \limits_a^b {f^2}\left( y \right)dy\)
-
Câu 5:
Gọi D là hình phẳng giới hạn bởi các đường y = 2x, y = 0, x = 0 và x = 2.Thể tích V của khối tròn xoay tạo thành khi quay D quanh trục Ox )được xác định bởi công thức:
A. \(V = \pi \mathop \smallint \limits_0^2 {2^{x + 1}}dx\)
B. \( V = \mathop \smallint \limits_0^2 {2^{x + 1}}dx\)
C. \( V = \mathop \smallint \limits_0^2 {4^x}dx\)
D. \( V = \pi \mathop \smallint \limits_0^2 {4^x}dx\)
-
Câu 6:
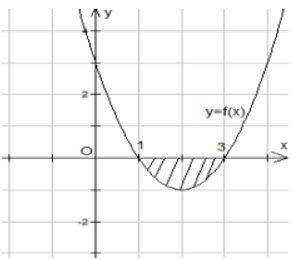
Cho hàm số y=f( x) liên tục và có đồ thị như hình bên. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số đã cho và trục Ox. Quay hình phẳng D quanh trục Ox ta được khối tròn xoay có thể tích V được xác định theo công thức
A. \( V = {\pi ^2}\mathop \smallint \limits_1^3 {\left[ {f\left( x \right)} \right]^{\,2}}{\mkern 1mu} {\rm{d}}x.\)
B. \( V = \mathop \smallint \limits_1^3 {\left[ {f\left( x \right)} \right]^{\,2}}{\mkern 1mu} {\rm{d}}x.\)
C. \( V = \frac{1}{3}\mathop \smallint \limits_1^3 {\left[ {f\left( x \right)} \right]^{\,2}}{\mkern 1mu} {\rm{d}}x.\)
D. \( V = \pi \mathop \smallint \limits_1^3 {\left[ {f\left( x \right)} \right]^{\,2}}{\mkern 1mu} {\rm{d}}x.\)
-
Câu 7:
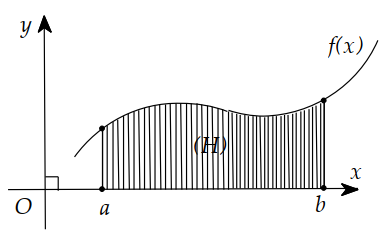
Cho hàm số y=f(x) liên tục trên đoạn ( a;b )và \(f(x)>0, \forall x \in (a;b )\). Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và 2 đường thẳng x=a, x=b ,(a<b). Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức:
A. \(\)
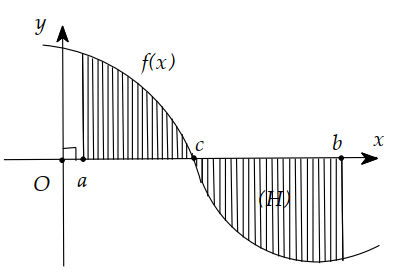
B. \( \pi \mathop \smallint \limits_a^b f({x^2})dx\)
C. \( \pi \mathop \smallint \limits_a^b {\left( {f(x)} \right)^2}dx\)
D. \( \mathop \smallint \limits_a^b {\left( {f(x)} \right)^2}dx\)
-
Câu 8:
Cho hình (H) giới hạn bởi đồ thị hàm số y = x3, trục hoành và hai đường thẳng x = 0,x = 1. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Ox được tính bởi:
A. \( V = {\pi ^2}\mathop \smallint \limits_0^1 {x^3}dx\)
B. \( V = {\pi}\mathop \smallint \limits_0^1 {x^3}dx\)
C. \( V = {\pi}\mathop \smallint \limits_0^1 {x^6}dx\)
D. \( V = {\pi ^2}\mathop \smallint \limits_0^1 {x}dx\)
-
Câu 9:
Cho hàm số y=f( x ) liên tục trên đoạn [ a;b ]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f( x ), trục hoành và hai đường thẳng x=a,x=b ( a<b ). Thể tích của khối của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:
A. \( V = \pi \mathop \smallint \limits_a^b {f^2}\left( x \right)dx\)
B. \( V = 2\pi \mathop \smallint \limits_a^b {f^2}\left( x \right)dx\)
C. \(V = {\pi ^2}\mathop \smallint \limits_a^b {f^2}\left( x \right)dx\)
D. \(V = {\pi ^2}\mathop \smallint \limits_a^b f\left( x \right)dx\)
-
Câu 10:
Cho hình ( H ) giới hạn bởi đồ thị hàm số y = f( x ) , trục hoành và hai đường thẳng x = a,x = b. Thể tích khối tròn xoay tạo thành khi quay ( H ) quanh trục (Ox ) là:
A. \( V = \pi \mathop \smallint \limits_a^b \left| {f\left( x \right)} \right|dx\)
B. \( V = \mathop \smallint \limits_a^b \left| {f\left( x \right)} \right|dx\)
C. \( V = \pi \mathop \smallint \limits_a^b {f^2}\left( x \right)dx\)
D. \( V = \pi ^2\mathop \smallint \limits_a^b {f^2}\left( x \right)dx\)
-
Câu 11:
Trên mặt phẳng Oxy, cho hình phẳng ( ) H giới hạn bởi các đường \(\begin{aligned} &(P): y=x^{2},\left(P^{\prime}\right): y=4 x^{2} \text { và } \text { (d): } y=4 \end{aligned}\) . Thể tích của khối tròn xoay khi quay (H ) quanh trục
Ox bằngA. \(\frac{9 \pi}{5}\)
B. \(\frac{4 \pi}{5}\)
C. \(\frac{7 \pi}{5}\)
D. \(2 \pi\)
-
Câu 12:
Quay hình phẳng ( H) như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn xoay có thể tích là
A. \(V=3 \pi^{2}\)
B. \(V=\pi^{2}\)
C. \(V=\frac{2 \pi^{2}}{3}\)
D. \(V=2 \pi^{2}\)
-
Câu 13:
Quay hình phẳng (H) như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn xoay có thể tích là
A. \(V=\frac{46 \pi}{9}\)
B. \(V=\frac{46 \pi}{15}\)
C. \(V=\frac{23 \pi}{9}\)
D. \(V=13 \pi\)
-
Câu 14:
Quay hình phẳng (H) như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn xoay
có thể tích làA. \(V=4 \sqrt{3} \pi\)
B. \(V=6 \sqrt{3} \pi\)
C. \(V=5 \sqrt{3} \pi\)
D. \(V=2 \sqrt{3} \pi\)
-
Câu 15:
Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường \(y=\sqrt{x+1}\) và trục Ox quay quanh trục Ox biết đáy lọ và miệng lọ có đường kính lần lượt là 2dm và 4dm, khi đó thể tích của lọ là:
A. \(8 \pi \mathrm{dm}^{3}\)
B. \(\frac{15}{2} \pi \mathrm{dm}^{3}\)
C. \(\frac{14}{3} \pi \mathrm{dm}^{3}\)
D. \(\frac{15}{2} \mathrm{dm}^{3}\)
-
Câu 16:
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường \(y=1-x^{2}, y=0\) quanh trục Ox có kết quả dạng \(\frac{a \pi}{b} ;(a ; b \in \mathbb{Z}) ; \frac{a}{b}\) là phân số tối giản. Khi đó a + b có kết quả là:
A. -15
B. 30
C. 31
D. -16
-
Câu 17:
Khối tròn xoay do hình giới hạn bởi các đường \(y=f(x), y=0, x=a, x=b,(a<b)\) quay quanh trục Ox có thể tích là V1 . Khối tròn xoay do hình giới hạn bởi các đường \(y=-3 f(x), y=0, x=a, x=b,(a<b)\)quay quanh trục Ox có thể tích là V2 . Chọn phương án đúng.
A. \(V_{1}=9 V_{2}\)
B. \(6 . V_{1}=V_{2}\)
C. \(V_{1}=V_{2}\)
D. \(9 . V_{1}=V_{2}\)
-
Câu 18:
Trên mặt phẳng Oxy, cho hình phẳng ( H) giới hạn bởi các đường \(y=3 x-x^{2}\) và trục hoành. Thể tích của khối tròn xoay khi quay (H ) quanh trục Ox bằng
A. \(\frac{9 \pi}{2}\)
B. \(\frac{81 \pi}{10}\)
C. \(\frac{7 \pi}{6}\)
D. \(9 \pi\)
-
Câu 19:
Thể tích của khối tròn xoay khi quay hình phẳng D giới hạn bởi các đường \(y=\sqrt{x}\) và y=x quanh trục Ox bằng
A. \(\pi \int_{0}^{1}(\sqrt{x}-x) \mathrm{d} x\)
B. \(\pi \int_{0}^{1}(x-\sqrt{x}) \mathrm{d} x\)
C. \(\pi \int_{0}^{1}\left(x-x^{2}\right) \mathrm{d} x\)
D. \(\pi \int_{0}^{1}\left(x^{2}-x\right) \mathrm{d} x\)
-
Câu 20:
Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi đường elip ( E) : \(x^{2}+9 y^{2}=9\) quay quanh Ox bằng
A. \(\pi\)
B. \(2\pi\)
C. \(3\pi\)
D. \(4\pi\)
-
Câu 21:
Thể tích khối tròn xoay sinh bởi khi quay hình phẳng giới hạn bởi các đồ thị hàm số \(y=2 x-x^{2}, y=x\) , quanh trục Ox là
A. \(V=\frac{1}{5}\)
B. \(V=\frac{\pi}{5}\)
C. \(V=\frac{1}{6}\)
D. \(V=\frac{\pi}{6}\)
-
Câu 22:
Cho hàm số \(y=(x-2)^{2}\) có đồ thị (C) , khối tròn xoay tạo thành khi quay hình phẳng giới
hạn bởi (C) , trục Ox , trục Oy và đường thẳng x = 3 có thể tích làA. \(V=\frac{33}{5}\)
B. \(V=\frac{34 \pi}{5}\)
C. \(V=\frac{32 \pi}{5}\)
D. \(V=\frac{33 \pi}{5}\)
-
Câu 23:
Cho hàm số \(y=4-x^{4}\) có đồ thị (C) , khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi (C) và trục Ox , quanh trục Oy có thể tích là
A. \(V=\frac{32 \pi}{3}\)
B. \(V=\frac{16 \pi}{3}\)
C. \(V=\frac{1024 \sqrt{2} \pi}{45}\)
D. \(V=\frac{\left(16-2(4-\sqrt{2})^{\frac{3}{2}}\right) \pi}{3}\)
-
Câu 24:
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số \(y=\frac{1}{x}\), trục Ox và hai đường thẳng \(x=1, x=2\). Khối tròn xoay tạo thành khi quay hình phẳng (H) quanh trục Ox có thể tích là
A. \(V=\frac{7 \pi}{3}\)
B. \(V=\ln 2\)
C. \(V=\frac{\pi}{2}\)
D. \(V=\pi \cdot \ln 2\)
-
Câu 25:
Cho hình phẳng ( H) giới hạn bởi đồ thị hàm số \(y=x(2-x)\) và trục Ox . Khối tròn xoay tạo thành khi quay hình phẳng (H) quanh trục Ox có thể tích là
A. \(V=\frac{4 \pi}{3}\)
B. \(V=\frac{16 \pi}{15}\)
C. \(V=\frac{512 \pi}{15}\)
D. \(V=\frac{\pi}{5}\)
-
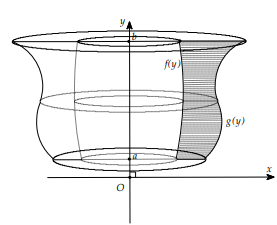
Câu 26:
Cho hình phẳng giới hạn (H) như hình vẽ bên. Thể tích khối tròn xoay sinh ra khi quay hình phẳng (H) quanh trục Oy là
A. \(V=\pi \int_{a}^{b}\left[g^{2}(y)-f^{2}(y)\right] \mathrm{d} x\)
B. \(V=\pi \int_{a}^{b}\left[f^{2}(y)-g^{2}(y)\right] \mathrm{d} y\)
C. \(V=\pi \int_{b}^{a}\left[g^{2}(y)-f^{2}(y)\right] \mathrm{d} y\)
D. \(V=\pi \int_{a}^{b}\left[f^{2}(y)+g^{2}(y)\right] \mathrm{d} y\)
-
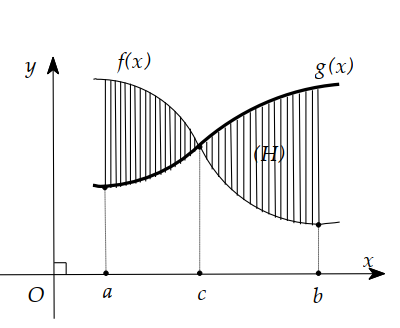
Câu 27:
Cho hình phẳng giới hạn (H) như hình vẽ bên. Thể tích khối tròn xoay sinh ra khi quay hình phẳng (H) quanh trục Ox là
A. \(\begin{aligned} &V=\pi \int_{a}^{b}\left[f^{2}(x)-g^{2}(x)\right] \mathrm{d} x \end{aligned}\)
B. \(V=\pi \int_{a}^{b}\left[g^{2}(x)-f^{2}(x)\right] \mathrm{d} x\)
C. \(\begin{array}{l} V=\pi \int_{a}^{c}\left[f^{2}(x)-g^{2}(x)\right] \mathrm{d} x+\pi \int_{c}^{b}\left[g^{2}(x)-f^{2}(x)\right] \mathrm{d} x \end{array}\)
D. \(V=\pi \int_{a}^{c}\left[g^{2}(x)-f^{2}(x)\right] \mathrm{d} x+\pi \int_{c}^{b}\left[f^{2}(x)-g^{2}(x)\right] \mathrm{d} x\)
-
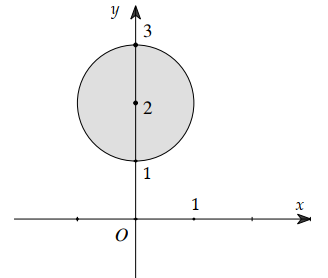
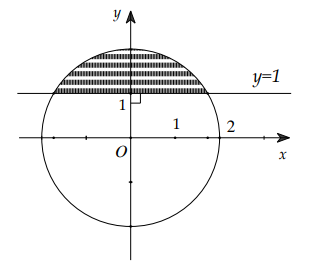
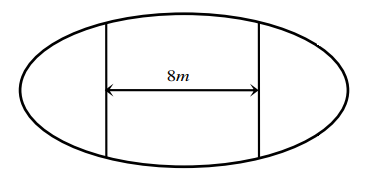
Câu 28:
Ông An có một mảnh vườn hình elip có độ dài trục lớn bằng 16m và độ dài trục bé bằng 10m . Ông muốn trồng hoa trên một dải đất rộng 8m và nhận trục bé của elip làm trục đối xứng (như hình vẽ). Biết kinh phí để trồng hoa là 100.000 đồng/1m2 . Hỏi ông An cần bao nhiêu tiền để trồng hoa trên dải đất đó? (Số tiền được làm tròn đến hàng nghìn).
A. 7.862.000 đồng.
B. 7.653.000 đồng
C. 7.128.000 đồng.
D. 7.826.000 đồng.
-
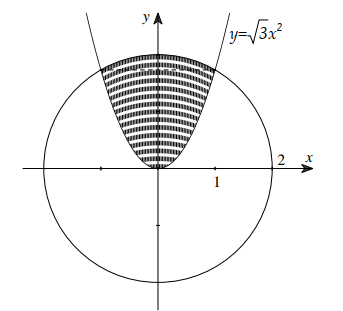
Câu 29:
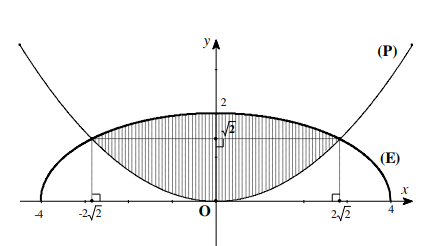
Hình phẳng (H) giới hạn bởi các đồ thị \(y=\sqrt{4-\frac{x^{2}}{4}}, y=\frac{x^{2}}{4 \sqrt{2}}\) (hình vẽ bên dưới). Khẳng định nào sau đây đúng?
A. \(\begin{array}{l} S=2 \int \limits_{0}^{2 \sqrt{2}}\left(\frac{x^{2}}{4 \sqrt{2}}-\sqrt{4-\frac{x^{2}}{4}}\right) \mathrm{d} x \end{array}\)
B. \(S=2 \int\limits_{-2 \sqrt{2}}^{0}\left(\frac{x^{2}}{4 \sqrt{2}}-\sqrt{4-\frac{x^{2}}{4}}\right) \mathrm{d} x \)
C. \(S=\int \limits_{-2 \sqrt{2}}^{2 \sqrt{2}}\left(\frac{x^{2}}{4 \sqrt{2}}-\sqrt{4-\frac{x^{2}}{4}}\right) \mathrm{d} x \)
D. \(S=\int\limits_{-2 \sqrt{2}}^{2 \sqrt{2}}\left(\sqrt{4-\frac{x^{2}}{4}}-\frac{x^{2}}{4 \sqrt{2}}\right) \mathrm{d} x\)
-
Câu 30:
Diện tích hình phẳng giới hạn bởi các đường \(y=\left|x^{2}-4 x+3\right|, y=x+3 \text { là } S=\frac{a}{b}, (a ; b \in \mathbb{Z} ; a \neq 0) ; \frac{a}{b}\) là phân số tối giản. Khẳng định nào sau đây là đúng?
A. \(b-a+103=0\)
B. \(b a+654=0\)
C. \(\frac{b^{2}}{a}=\frac{25}{109}\)
D. \(b-a^{3}+107=0\)
-
Câu 31:
Diện tích hình phẳng giới hạn bới các đường \(y=\frac{-3 x-1}{x-1}, O x, O y\) là
A. \(S=4 \ln \frac{4}{3}+1\)
B. \(S=4 \ln \frac{4}{3}\)
C. \(S=4 \ln \frac{4}{3}-1\)
D. \(S=4 \ln \frac{4}{3}+2\)
-
Câu 32:
Hình phẳng giới hạn bởi đồ thị hàm số \(y=\frac{10}{3} x-x^{2} \text { và } y=\left\{\begin{array}{ll} -x & \text { khi } x \leq 1 \\ x-2 & \text { khi } x>1 \end{array}\right.\) có diện tích là:
A. \(S=13\)
B. \(S=7\)
C. \(\begin{aligned} &S=\frac{15}{2} \end{aligned}\)
D. \(S=\frac{13}{2}\)
-
Câu 33:
Hình phẳng giới hạn bởi đồ thị hàm số \(y=x^{3}-2 x\) và đường thẳng \(2 x-y=0\) có diện tích là
A. S=8
B. S=2
C. S=4
D. S=16
-
Câu 34:
Hình phẳng giới hạn bởi đồ thị hàm số \(y=1-\frac{1}{x^{2}}\), trục Ox và hai đường thẳng \(x=\frac{1}{2}, x=2\) có diện tích là
A. \(S=5\)
B. \(S=\frac{5}{2}\)
C. \(S=1\)
D. \(S=2\)
-
Câu 35:
Hình phẳng giới hạn bởi đồ thị hàm số \(y=x^{3}\) , trục Ox và đường thẳng x =-2 có diện tích là
A. S=1
B. S=16
C. S=4
D. \(S=4\pi\)
-
Câu 36:
Hình phẳng giới hạn bởi đường elip \((E): x^{2}+16 y^{2}=16\) có diện tích bằng
A. \(\pi\)
B. \(2\pi\)
C. \(3\pi\)
D. \(4\pi\)
-
Câu 37:
Diện tích hình phẳng giới hạn bởi các đường \(y=x^{2}-2 x+1, y=-x+1, x=0, x=m,(m<0)\) bằng \(\frac{5}{6}\). Khi đó giá trị m bằng:
A. -3
B. -2
C. -1
D. -4
-
Câu 38:
Diện tích hình phẳng giới hạn bởi các đường \(y=x^{2}-2 x+1, y=x+1, x=0, x=m,(0<m<3)\) bằng:
A. \(\frac{m^{3}}{3}-\frac{3 m^{2}}{2}\)
B. \(-\frac{m^{3}}{3}+\frac{3 m^{2}}{2}\)
C. \(\frac{m^{3}}{3}-\frac{m^{2}}{2}+2 m\)
D. \(\frac{m^{3}}{3}-\frac{m^{2}}{2}-2 m\)
-
Câu 39:
Gọi S là diện tích hình phẳng giới hạn bởi các đường \(y=-x^{2}-2 x+1, y=m,(m>2), x=0, x=1\). Tìm m sao cho S=48m=6
A. m=10
B. m=6
C. m=4
D. m=8
-
Câu 40:
Diện tích hình phẳng giới hạn bởi các đường \(y=x^{2}-4 x+1, y=m,(m \leq-3), x=0, x=3\) là:
A. \(3 m+6\)
B. \(-3 m+6\)
C. \(3 m-6\)
D. \(-3 m-6\)
-
Câu 41:
Tính diện tích hình phẳng giới hạn bởi các đường \(y=e^{x} ; y=e^{-x} ; x=1\)
A. \(\frac{e^{2}+2 e+1}{e}\)
B. \(\frac{e^{2}-2 e+1}{e}\)
C. \(\frac{e^{2}+2 e-1}{e}\)
D. \(\frac{e^{2}-2 e-1}{e}\)
-
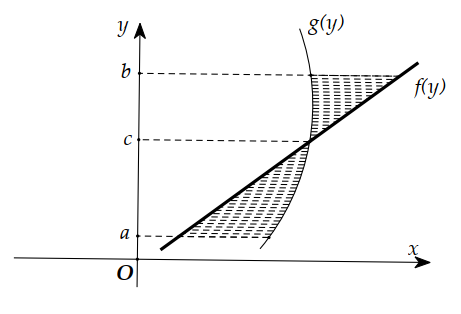
Câu 42:
Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(x=f(y), x=g(y)\) và hai đường thẳng \(y=a, y=b\), như hình vẽ bên. Khẳng định nào sau đây đúng?
A. \(\begin{array}{l} S=\int_{a}^{c}[g(y)-f(y)] \mathrm{d} x+\int_{c}^{b}[f(y)-g(y)] \mathrm{d} x \end{array}\)
B. \(S=\left|\int_{a}^{b}[f(y)+g(y)] \mathrm{d} y\right|\)
C. \(S=\int_{a}^{c}[g(y)-f(y)] \mathrm{d} y+\int_{c}^{b}[f(y)-g(y)] \mathrm{d} y\)
D. \(S=\left|\int_{a}^{b}[f(y)-g(y)] \mathrm{d} y\right|\)
-
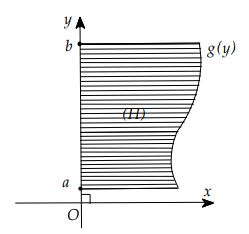
Câu 43:
Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(x=g(y)\), trục tung và hai đường thẳng \(y=a, y=b\) , như hình vẽ bên. Khẳng định nào sau đây đúng?
A. \(S=\int_{a}^{b} g(y) \mathrm{d} x \)
B. \(S=\int_{b}^{a}|g(y)| \mathrm{d} y \)
C. \(S=\int_{a}^{b} g(y) \mathrm{d} y\)
D. \(S=\left|\int_{a}^{b} g(y) \mathrm{d} x\right|\)
-
Câu 44:
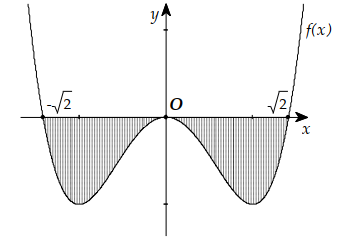
Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y=f(x)=x^{4}-2 x^{2}\)2 và
trục hoành như hình vẽ bên. Khẳng định nào sau đây sai?A. \(S=\int_{-\sqrt{2}}^{\sqrt{2}}|f(x)| \mathrm{d} x\)
B. \(S=2 \int_{0}^{\sqrt{2}} f(x) \mathrm{d} x\)
C. \(S=2 \int_{0}^{\sqrt{2}}[-f(x)] \mathrm{d} x\)
D. \(S=\int_{-\sqrt{2}}^{0}[-f(x)] \mathrm{d} x+\int_{0}^{\sqrt{2}}[-f(x)] \mathrm{d} x\)
-
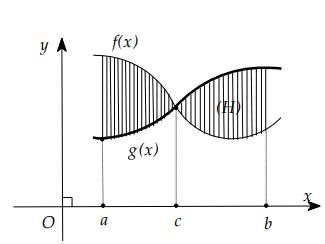
Câu 45:
Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y=f(x), y=g(x)\) và hai đường thẳng \(x=a, x=b\) , như hình vẽ bên. Khẳng định nào sau đây đúng?
A. \(\begin{array}{l} S=\int_{a}^{c}[g(x)-f(x)] \mathrm{d} x+\int_{c}^{b}[f(x)-g(x)] \mathrm{d} x \end{array}\)
B. \(S=\left|\int_{a}^{b}[f(x)+g(x)] \mathrm{d} x\right| \)
C. \(S=\int_{a}^{c}[f(x)-g(x)] \mathrm{d} x+\int_{c}^{b}[g(x)-f(x)] \mathrm{d} x \)
D. \(S=\left|\int_{a}^{c} f(x) \mathrm{d} x+\int_{c}^{b} g(x) \mathrm{d} x\right|\)
-
Câu 46:
Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y=f(x), y=g(x)\) và hai đường thẳng \(x=a, x=b\), như hình vẽ bên. Khẳng định nào sau đây đúng?
A. \(S=\left|\int_{a}^{b} g(x) \mathrm{d} x\right|-\left|\int_{a}^{b} f(x) \mathrm{d} x\right|\)
B. \(S=\int_{a}^{b} f(x) \mathrm{d} x-\int_{a}^{b} g(x) \mathrm{d} x\)
C. \(S=\int_{a}^{b} g(x) \mathrm{d} x-\int_{a}^{b} f(x) \mathrm{d} x\)
D. \(S=\int_{a}^{b} f(x) \mathrm{d} x+\int_{a}^{b} g(x) \mathrm{d} x\)
-
Câu 47:
Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a, x=b\) , như hình vẽ bên. Khẳng định nào sau đây đúng?
A. \(\begin{aligned} S=\int_{a}^{b} f(x) \mathrm{d} x \end{aligned}\)
B. \(S=\left|\int_{a}^{b} f(x) \mathrm{d} x\right|\)
C. \(S=\int_{a}^{c} f(x) \mathrm{d} x-\int_{c}^{b} f(x) \mathrm{d} x \)
D. \( S=\int_{a}^{c} f(x) \mathrm{d} x+\int_{c}^{b} f(x) \mathrm{d} x\)
-
Câu 48:
Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a, x=b\) , như hình vẽ bên. Khẳng định nào sau đây đúng?
A. \(S=\int_{b}^{a} f(x) \mathrm{d} x\)
B. \(S=\int_{a}^{b}[-f(x)] \mathrm{d} x\)
C. \(S=\int_{b}^{a}|f(x)| \mathrm{d} x\)
D. \(S=\int_{a}^{b} f(x) \mathrm{d} x\)
-
Câu 49:
Diện tích hình phẳng giới hạn bởi \(y = x^2 , y = 0 , x = 1 , x = 2 \) bằng:
A. 4/3
B. 7/3
C. 8/3
D. 1
-
Câu 50:
Diện tích của hình phẳng giới hạn bởi các đường \(y = x^2+ 1 , y = 0, x = - 1, x = 2 \) bằng:
A. 3
B. 6
C. 4
D. 5



.PNG)