Trắc nghiệm Phép quay Toán Lớp 11
-
Câu 1:
Tìm ảnh của đường tròn (C):(x−1)2+(y+2)2=9(C):(x−1)2+(y+2)2=9 qua phép quay Q(I;900)Q(I;900) với I(3;4) .
A. (C′):(x+2)2+(y−2)2=9(C′):(x+2)2+(y−2)2=9
B. (C′):(x−3)2+(y+2)2=9(C′):(x−3)2+(y+2)2=9
C. (C′):(x+5)2+(y−7)2=9(C′):(x+5)2+(y−7)2=9
D. (C′):(x+3)2+(y−2)2=9(C′):(x+3)2+(y−2)2=9
-
Câu 2:
Tìm ảnh của đường thẳng d:5x−3y+15=0d:5x−3y+15=0 qua phép quayQ(0;90∘)Q(0;90∘)
A. d′:x+y+15=0d′:x+y+15=0
B. d′:3x+5y+5=0d′:3x+5y+5=0
C. d′:3x+y+5=0d′:3x+y+5=0
D. d′:3x+5y+15=0d′:3x+5y+15=0
-
Câu 3:
Cho I( 2;1) và đường thẳng d:2x+3y+4=0d:2x+3y+4=0 . Tìm ảnh của d qua Q(I;45∘)Q(I;45∘).
A. d′:−x+5y−3+√2=0d′:−x+5y−3+√2=0
B. d′:−x+5y−3=0d′:−x+5y−3=0
C. d′:−x+5y−10√2=0d′:−x+5y−10√2=0
D. d′:−x+5y−3+10√2=0d′:−x+5y−3+10√2=0
-
Câu 4:
Cho M(3;4) . Tìm ảnh của điểm M qua phép quay tâm O góc quay 300 .
A. M′(3√32;32+2√3)M′(3√32;32+2√3)
B. M′(−2;2√3)M′(−2;2√3)
C. M′(3√32;2√3)M′(3√32;2√3)
D. M′(3√32−2;32+2√3)M′(3√32−2;32+2√3)
-
Câu 5:
Trong mặt phẳng với hệ trục tọa độ Oxy , cho điểm M (2;0) và điểm N(0; 2) . Phép quay tâm O biến điểm M thành điển N , khi đó góc quay của nó là
A. φ=30∘φ=30∘
B. φ=45∘φ=45∘
C. φ=90∘φ=90∘
D. φ=270∘φ=270∘
-
Câu 6:
Trong mặt phẳng Oxy cho điểm A(3;0) . Tìm tọa độ ảnh A' của điểm A qua phép quay Q(O,π2)Q(O,π2)
A. A′(0;−3)A′(0;−3)
B. A′(0;3)A′(0;3)
C. A′(−3;0)A′(−3;0)
D. A′(2√3;2√3)A′(2√3;2√3)
-
Câu 7:
Trong mặt phẳng Oxy , cho điểm M(1;1). Hỏi các điểm sau điểm nào là ảnh của M qua phép quay tâm O , góc 450450 ?
A. M′(−1;1)M′(−1;1)
B. M′(1;0)M′(1;0)
C. M′(√2;0)M′(√2;0)
D. M′(0;√2)M′(0;√2)
-
Câu 8:
Phép quay Q(O;φ)Q(O;φ) biến điểm M thành M′.M′. Khi đó
A. →OM=→OM′;(OM,OM′)=φ−−→OM=−−−→OM′;(OM,OM′)=φ
B. OM=OM′;(OM,OM′)=φOM=OM′;(OM,OM′)=φ
C. →OM=→OM′;^MOM′=φ−−→OM=−−−→OM′;ˆMOM′=φ
D. OM=OM′;^MOM′=φOM=OM′;ˆMOM′=φ
-
Câu 9:
Có bao nhiêu điềm biến thành chính nó qua phép quay tâm O góc quay α≠k2π(k∈Z)?α≠k2π(k∈Z)?
A. Không có
B. Một
C. Hai
D. Vô số.
-
Câu 10:
Cho hình chữ nhật có O là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm O góc quay α,0<α≤2πα,0<α≤2π biến hình chữ nhật trên thành chính nó?
A. Không có
B. hai
C. ba
D. bốn
-
Câu 11:
Cho hình vuông tâm O . Hỏi có bao nhiêu phép quay tâm O góc quay α,0<α≤2πα,0<α≤2π biến hình vuông trên thành chính nó?
A. 1
B. 2
C. 3
D. 4
-
Câu 12:
Cho tam giác đều tâm O . Hỏi có bao nhiêu phép quay tâm O góc quay α,0<α≤2πα,0<α≤2π biến tam giác trên thành chính nó?
A. 2
B. 1
C. 3
D. 4
-
Câu 13:
Trong mặt phẳng tọa độ Oxy cho hai đường thẳng a và b có phương trình lần lượt là 4x+3y+5=0 và x+7y−4=04x+3y+5=0 và x+7y−4=0. Nếu có phép quay biến đường thẳng này thành đường thẳng kia thì số đo của góc quay φ(0≤φ≤1800)φ(0≤φ≤1800) là:
A. 45∘45∘
B. 60∘60∘
C. 90∘90∘
D. 120∘
-
Câu 14:
Trong mặt phẳng với hệ tọa độ Oxy cho hai đường thẳng a và b có phương trình lần lượt là 2x+y+5=0 và x−2y−3=0. Nếu có phép quay biến đường thẳng này thành đường thẳng kia thì số đo của góc quay φ(0≤φ≤1800) là:
A. 45∘
B. 60∘
C. 90∘
D. 120∘
-
Câu 15:
Trong mặt phẳng tọa độ Oxy cho điểm M (1;1). Hỏi các điểm sau điểm nào là ảnh của M qua phép quay tâm O góc quay φ=450?
A. M′1(−1;1)
B. M′2(1;0)
C. M′3(√2;0)
D. M′4(0;√2)
-
Câu 16:
Trong mặt phẳng tọa độ Oxy cho hai điểm M (2;0) và N (0;2). Phép quay tâm O biến điểm M thành điểm N , khi đó góc quay của nó là:
A. φ=30∘
B. φ=30∘hoặcφ=45∘
C. φ=90∘
D. φ=90∘hoặcφ=270∘.
-
Câu 17:
Trong mặt phẳng tọa độ Oxy cho phép quay tâm O biến điểm A(1;0) thành điểm A'(0;1) Khi đó nó biến điểm M (1; -1) thành điểm:
A. M′(−1;−1)
B. M′(1;1)
C. M′(−1;1)
D. M′(1;0)
-
Câu 18:
Trong mặt phẳng tọa độ o điểm A(3;0). Tìm tọa độ điểm A′ là ảnh của điểm A qua phép quay tâm O(0;0) góc quay π2
A. A′(0;−3)
B. A′(0;3)
C. A′(−3;0)
D. A′(2√3;2√3)
-
Câu 19:
Cho phép quay Q(O,φ) biến điểm A thành điểm A' và biến điểm M thành điểm M '. Mệnh đề nào sau đây là sai?
A. →AM=→A′M′
B. (^OA,OA′)=^(OM,OM′)=φ
C. (→AM,→A′M′)=φ(0≤φ≤π)
D. AM=A′M′
-
Câu 20:
Cho hai đường thẳng bất kỳ d và d' . Có bao nhiêu phép quay biến đường thẳng d thành đường thẳng d ' ?
A. 0
B. 1
C. 2
D. Vô số.
-
Câu 21:
Cho tam giác ABC vuông tại B và góc tại A bằng 60∘ (các đỉnh của tam giác ghi theo ngược chiều kim đồng hồ). Về phía ngoài tam giác vẽ tam giác đều ACD. Ảnh của cạnh BC qua phép quay tâm A góc quay 60∘ là:
A. AD.
B. AI với I là trung điểm của CD.
C. CJ với J là trung điểm của AD
D. DK với K là trung điểm của AC.
-
Câu 22:
Cho tam giác đều ABC có tâm O và các đường cao AA′,BB′,CC′ (các đỉnh của tam giác ghi theo chiều kim đồng hồ). Ảnh của đường cao AA' qua phép quay tâm O góc quay 2400 là:
A. AA'
B. BB'
C. CC'
D. BC
-
Câu 23:
Cho hình thoi ABCD có góc ^ABC=60∘ (các đỉnh của hình thoi ghi theo chiều kim đồng hồ). Ảnh của cạnh CD qua phép quay Q(A,600) là:
A. AB
B. BC
C. CD
D. DA
-
Câu 24:
Cho hình chữ nhật tâm O. Hỏi có bao nhiêu phép quay tâm O góc α với 0≤α<2π , biến hình chữ nhật trên thành chính nó?
A. 0
B. 2
C. 3
D. 4
-
Câu 25:
Cho hình vuông tâm O. Hỏi có bao nhiêu phép quay tâm O góc α với 0≤α<2π , biến hình vuông trên thành chính nó?
A. 1
B. 2
C. 3
D. 4
-
Câu 26:
Cho hình vuông tâm O. Xét phép quay Q có tâm quay O và góc quay φ . Với giá trị nào sau đây của φ, phép quay Q biến hình vuông thành chính nó?
A. φ=π6
B. φ=π4
C. φ=π3
D. φ=π2
-
Câu 27:
Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O góc αvới 0≤α<2π , biến tam giác trên thành chính nó?
A. 1
B. 2
C. 3
D. 4
-
Câu 28:
Cho tam giác đều ABC. Hãy xác định góc quay của phép quay tâm A biến B thành C .
A. φ=30∘
B. φ=90∘
C. φ=−120∘
D. φ=60∘hoặcφ=−60∘
-
Câu 29:
Cho tam giác đều tâm O. Với giá trị nào dưới đây của φ thì phép quay Q(O,φ) biến tam giác đều thành chính nó?
A. φ=π3
B. φ=2π3
C. φ=3π2
D. φ=π2
-
Câu 30:
Có bao nhiêu điểm biến thành chính nó qua phép quay tâm O góc α với α≠k2π ( k là một số nguyên)?
A. 0
B. 1
C. 2
D. Vô số.
-
Câu 31:
Trong mặt phẳng tọa độ Oxy cho điểm A(3;4). Gọi A' là ảnh của điểm A qua phép quay tâm O(0;0) góc quay 900. Điểm A' có tọa độ là:
A. (-3;4)
B. (-4;-3)
C. (3;-4)
D. (-4;3)
-
Câu 32:
Trong phép quay Q60∘O, điểm M (1;0) cho ảnh là điểm nào sau đây?
A. M'(-1;0)
B. M'(12;√32)
C. M'(√32;12)
D. Kết quả khác
-
Câu 33:
Cho đường tròn (C):(x−2)2+(y−2)2 = 4. Phép quay tâm O góc quay 450 biến (C) thành (C'). Khi đó phương trình của (C') là:
A. (x−2√2)2+y2=4
B. x2+(y−2√2)2=4
C. x2+y2=4
D. x2+(y−2)2=4
-
Câu 34:
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình (x − 3)2 + y2 = 4. Phép quay tâm O(0;0) góc quay 90o biến (C) thành (C’) có phương trình:
A. x2 + y2 − 6x + 5 = 0
B. x2 + y2 − 6y + 6 = 0
C. x2 + y2 + 6x − 6 = 0
D. x2 + y2 − 6y + 5 = 0
-
Câu 35:
Trong mặt phẳng Oxy phép quay Q(O; 90o) biến đường thẳng d có phương trình: 2x - y + 1 = 0 thành đường thẳng d’ có phương trình.
A. x + 2y - 1 = 0
B. 2x + y + 1 = 0
C. 2x - y + 1 = 0
D. x + 2y + 1 = 0
-
Câu 36:
Trong mặt phẳng Oxy phép quay Q(O; 90o) biến đường thẳng d có phương trình x - 2y = 0 thành đường thẳng d’ có phương trình:
A. x + 2y = 0
B. 2x + y = 0
C. 2x - y = 0
D. x - y + 2 = 0
-
Câu 37:
Trong mặt phẳng Oxy phép quay tâm K, góc 60o60o biến M(1;1) thành M’(-1;1). Tọa độ điểm K là:
A. (0;0)
B. (0;−√3)
C. (0;1−√3)
D. (√2;0)
-
Câu 38:
Trong mặt phẳng Oxy cho điểm M(1;1). Điểm nào sau đây là ảnh của M qua phép quay tâm O, góc quay 45o.
A. (0;√2)
B. (- 1;1)
C. (1;0)
D. (√2;0)
-
Câu 39:
Trong mặt phẳng Oxy qua phép quay Q(O; 90o) thì M'(2; -3) là ảnh của điểm.
A. M(3;2)
B. M(2;3)
C. M(3;-2)
D. M(-3;-2)
-
Câu 40:
Trong mặt phẳng Oxy, ảnh của điểm M (- 6;1) qua phép quay Q(O; 90o) là:
A. M'(-1;-6)
B. M'(1;6)
C. M'(-6;-1)
D. M'(6;1)
-
Câu 41:
Cho ba điểm thẳng hàng A, B, C. dựng các tam giác đều ABD, BCE về cùng phía đối với đường thẳng AC. Gọi F, G lần lượt là trung điểm của các cạnh AE và DC. Tam giác BFG là:
A. tam giác thường
B. tam giác vuông đỉnh B
C. tam giác cân đỉnh B
D. tam giác đều
-
Câu 42:
Cho hình lục giác ABCDEF, tâm O. mệnh đề nào sau đây sai?
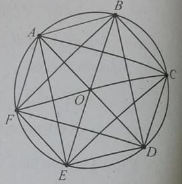
A. phép quay tâm O góc quay 60o biến tam giác BCD thành tam giác ABC.
B. phép quay tâm O góc quay 120o biến tam giác OEC thành tam giác OCA
C. phép quay tâm O góc quay −60o, biến tam giác AFD thành tam giác FEC.
D. phép quay tâm O góc quay −120o biến tam giác BCD thành tam giác DEF.
-
Câu 43:
Trong mặt phẳng tọa độ Oxy cho điểm M(1;0). Phép quay tâm O góc quay 45o biến M thành M’ có tọa độ
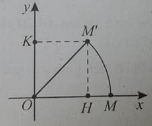
A. (√2;√2)
B. (√22;−√22)
C. (√2;−√2)
D. (√22;√22)
-
Câu 44:
Dựng ra phía ngoài tam giác vuông cân ABC đỉnh A các tam giác đều ABD và ACE. Góc giữa hai đường thẳng BE và CD là:
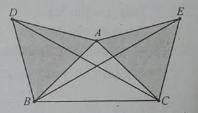
A. 900
B. 600
C. 450
D. 300
-
Câu 45:
Cho một tam giác ABC tâm O, gọi A, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Mệnh đề nào sau đây đúng?
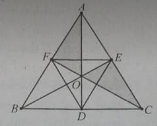
A. Q(O; 120o)(ΔODC) = ΔOFA
B. Q(O; 120o)(ΔAOF) = ΔBOD
C. Q(O; 120o)(ΔAOB) = ΔAOC
D. Q(O; 60o)(ΔOFE) = ΔODE
-
Câu 46:
Với giá trị nào của góc φ sau đây thì phép quay Q(O;φ) biến hình vuông ABCD tâm O thành chính nó?
A. φ=π2
B. φ=3π4
C. φ=2π3
D. φ=π3
-
Câu 47:
Trong mặt phẳng Oxy, thực hiện liên tiếp phép quay tâm O góc quay −45o và phép đối xứng tâm O thì điểm M(1;1) biến thành điểm M’’ có tọa độ là:
A. (-1;0)
B. (√2;0)
C. (√2;−√2)
D. (−√2;0)














