ADMICRO
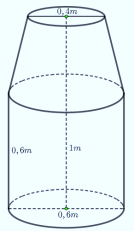
Tính thể tích của thùng đựng nước có hình dạng và kích thước như hình vẽ
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ZUNIA12
Lời giải:
Báo saiThể tích của thùng đựng nước là: V=V1+V2V=V1+V2 với V1V1 là thể tích khối trụ có đường kính đáy bằng 2R1=0,6m2R1=0,6m và chiều cao h1=0,6mh1=0,6m; V2V2 là thể tích khối nón cụt có đường kính đáy lớn 2R1=0,6m2R1=0,6m và đường kính đáy nhỏ 2R2=0,4m2R2=0,4m và chiều cao h2=1−0,6=0,4mh2=1−0,6=0,4m.
Khi đó: V1=πR21.h1=π.(0,3)2.0,6=27π500(m3)V1=πR21.h1=π.(0,3)2.0,6=27π500(m3)
V2=13πh2(R12+R22+R1R2)=13π.0,4.(0,09+0,04+0,06)=19π750(m3)
Vậy V=V1+V2=27π500+19π750=1991500π(m3)=0,238π3(m3).
ZUNIA9
AANETWORK