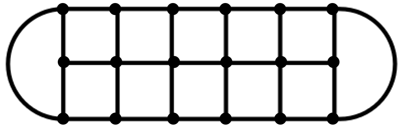
Gọi \(S\) là tập hợp gồm 18 điểm được đánh dấu trong bàn cờ ô ăn quan như nhìn bên. Chọn ngẫu nhiên 2 điểm thuộc \(S\), xác suất để đường thẳng đi qua hai điểm được chọn không chức cạnh của bất kì hình vuông nào trong ô bàn cờ là

Số nghiệm nguyên của bất phương trình \(\left( {{3}^{{{x}^{2}}-1}}-{{27}^{x+1}} \right)\left[ {{\log }_{3}}\left( x+8 \right)-2 \right]\le 0\) là

Giả sử \(z,w\) là hai số phức thỏa mãn \(\left| z \right|=\left| w \right|=\frac{5}{2},\,\,\,\left| z-w \right|=4\). Trên mặt phẳng \(Oxy\) gọi \(M,N\) lần lượt là điểm biểu diễn số phức \(z+w\) và \(3z+w\). Diện tích tam giác \(OMN\) bằng bao nhiêu.

Xét các số thực \(a\) thay đổi thỏa mãn \(\left| a \right|\le 2\) và \({{z}_{1}}\), \({{z}_{2}}\) là các nghiệm phức của phương trình \({{z}^{2}}-az+1=0\). Gọi \(A\left( \frac{7}{2};2 \right)\) và \(M\), \(N\) lần lượt là điểm biểu diễn số phức \({{z}_{1}}\) và \({{z}_{2}}\). Giá trị lớn nhất của diện tích tam giác \(AMN\) bằng

Đạo hàm của hàm số \(f\left( x \right)={{3}^{2-x}}\)

Cho mặt cầu có bán kính bằng \(3\). Một khối nón có chiều cao thay đổi sao cho đỉnh và đường tròn đáy cùng thuộc mặt cầu đã cho. Khi thể tích khối nón lớn nhất thì chiều cao của nó bằng

Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(\int\limits_{0}^{1}{f\left( 1-2x \right)}\,dx=\frac{1}{3}.\) Tích phân \(\int\limits_{-1}^{1}{f\left( x \right)}\,dx\) bằng

Trong không gian với hệ trục tọa độ \(Oxyz\), cho điểm \(A\left( 2\ ;\ 1\ ;\ 3 \right)\) và mặt phẳng \(\left( P \right):x+my+\left( 2m+1 \right)z-m-2=0\), với \(m\) là tham số. Gọi \(H\left( a;b;c \right)\) là hình chiếu vuông góc của điểm \(A\) trên \(\left( P \right)\). Khi khoảng cách từ điểm \(A\) đến \(\left( P \right)\) lớn nhất; tính \(a+b\).

Cho hàm số \(y=f\left( x \right)\) có đạo hàm \({f}'\left( x \right)={{x}^{2}}\left( {{x}^{2}}-4 \right),\forall x\in \mathbb{R}\). Hàm số đã cho đồng biến trên những khoảng nào dưới đây?

Trong không gian \(Oxyz\), cho hai điểm \(A\left( 1;1;2 \right)\) và \(B\left( -1;3;3 \right)\). Một véc-tơ chỉ phương của đường thẳng \(AB\) có tọa độ là

Cho hình lập phương \(ABCD.A'B'C'D'\) có độ dài cạnh bằng \(\sqrt{6}\). Khoảng cách giữa 2 đường thẳng \(BD\) và \(CC'\) bằng

Cho \(\int\limits_{0}^{2}{f\left( x \right)dx}=4\); \(\int\limits_{0}^{2}{g\left( x \right)dx}=1\). Tích phân \(\int\limits_{0}^{2}{\left[ f\left( x \right)-2g\left( x \right) \right]dx}\) bằng

Trong không gian \(Oxyz,\) mặt phẳng đi qua ba điểm \(A\left( 1;-2;1 \right),\,\,B\left( 4;-5;1 \right)\) và \(C\left( 2;0;2 \right)\) có phương trình là

Gọi \(m\) là giá trị nhỏ nhất của hàm số \(f(x)=\frac{ax+32-a}{{{2}^{x}}},(a\in \mathbb{R})\) trên đoạn \(\left[ -2;1 \right]\). Hỏi có bao nhiêu số nguyên đương \(a\) để \(m\ge 16?\)

Giả sử \(a\), \(b\) là các số thực dương tùy ý, \({{\log }_{4}}\left( {{a}^{6}}{{b}^{2}} \right)\) bằng

Giả sử \(a,b\) là các số thực dương. Gọi \({{V}_{1}}\) là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường thẳng \(y=a\sqrt{x}\), \(y=0\), \(x=1\) quanh trục \(Ox\); \({{V}_{2}}\) là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường thẳng \(y=b{{x}^{2}},y=0,x=1\) quanh trục \(Ox\). Biết \({{V}_{2}}=10{{V}_{1}}\), giá trị \(\frac{a}{b}\) bằng

Một khối trụ có bán kính đáy bằng \(2\) và chiều cao bằng \(3\). Thể tích khối trụ bằng

Cho hàm số bậc bốn \(y=f\left( x \right)\) có đồ thị như hình bên. Hỏi phương trình \(f\left( 1-x \right)=1\) có bao nhiêu nghiệm thuộc khoảng \(\left( 0;\,+\infty  \right)\)?

Cho số phức \(z=\,2-3i\). Điểm biểu diễn của số phức \(\overline{z}\) là

Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B,\,AB=1\) và \(AC=2\). Cạnh bên \(SA\) vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng \(\left( SAC \right)\) và \(\left( SBC \right)\) bằng \({{60}^{0}}\). Thể tích của khối chóp \(S.ABC\) bằng

Diện tích của mặt cầu có bán kính bằng \(5\) là