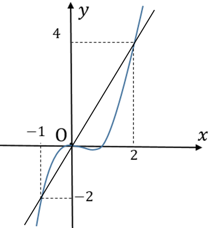
Cho hàm số bậc bốn \(y=f\left( x \right)\) có đồ thị hàm số \(y={f}'\left( x \right)\) như hình bên. Hỏi hàm số \(g\left( x \right)=f\left( x+1 \right)-{{x}^{2}}-2x\) đồng biến trên khoảng nào sau đây?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn D
Ta có \({g}'\left( x \right)={f}'\left( x+1 \right)-2x-2\).
Hàm số đồng biến ứng với \({g}'\left( x \right)\ge 0\)\( \Leftrightarrow {f}'\left( x+1 \right)\ge 2\left( x+1 \right)\,\,\,\left( 1 \right)\)
Đặt \(t=x+1\Rightarrow \left( 1 \right)\) thành \({f}'\left( t \right)\ge 2\left( t \right)\). Vẽ đường thẳng \(y=2x\) lên cùng hệ trục tọa độ với đồ thị hàm số \(y={f}'\left( x \right)\).
Từ đồ thị suy ra
\(\begin{array}{l} g'\left( x \right) \ge 0\\ \Leftrightarrow \left[ \begin{array}{l} - 1 \le t \le 0\\ t \ge 2 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} - 1 \le x + 1 \le 0\\ x + 1 \le 2 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} - 2 \le x \le - 1\\ x \ge 1 \end{array} \right.. \end{array}\)
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Trần Khai Nguyên



.PNG)
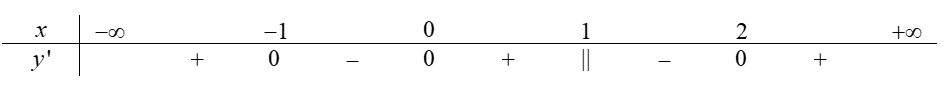
.PNG)











