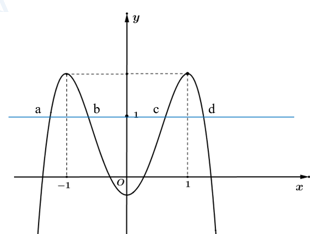
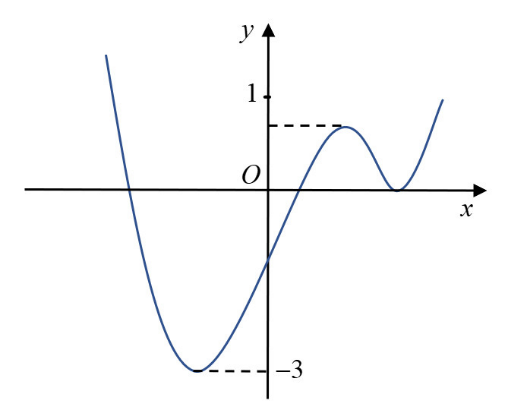
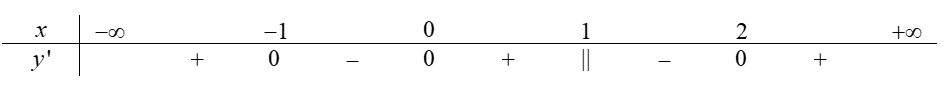Cho hàm số bậc bốn \(y=f\left( x \right)\) có đồ thị như hình bên. Hỏi phương trình \(f\left( 1-x \right)=1\) có bao nhiêu nghiệm thuộc khoảng \(\left( 0;\,+\infty  \right)\)?

Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B,\,AB=1\) và \(AC=2\). Cạnh bên \(SA\) vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng \(\left( SAC \right)\) và \(\left( SBC \right)\) bằng \({{60}^{0}}\). Thể tích của khối chóp \(S.ABC\) bằng

Cho khối lăng trụ \(ABC.{A}'{B}'{C}'\) có tất cả các cạnh bằng \(\sqrt{2}\). Cạnh bên tạo với mặt phẳng đáy góc \({{60}^{\circ }}\). Tính thể tích khối lăng trụ \(ABC.{A}'{B}'{C}'\).

Mệnh đề nào sau đây đúng?

Gọi \(\left( D \right)\) là hình phẳng giới hạn bởi các đường \(y=0,y=x\) và \(y=\sqrt{x+2}\). Diện tích \(S\) của \(\left( D \right)\) được tính theo công thức nào dưới đây?

Cho hàm số \(y=\,f(x)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm như hình dưới. Hàm số đã cho có bao nhiêu điểm cực trị?

Gọi \(m\) là giá trị nhỏ nhất của hàm số \(f(x)=\frac{ax+32-a}{{{2}^{x}}},(a\in \mathbb{R})\) trên đoạn \(\left[ -2;1 \right]\). Hỏi có bao nhiêu số nguyên đương \(a\) để \(m\ge 16?\)

Cho hình lập phương \(ABCD.A'B'C'D'\) có độ dài cạnh bằng \(\sqrt{6}\). Khoảng cách giữa 2 đường thẳng \(BD\) và \(CC'\) bằng

Cho hàm số \(y=f\left( x \right)\) có đạo hàm là \({f}'\left( x \right)=\left( {{x}^{2}}+9x \right)\left( {{x}^{2}}-9 \right),\)với mọi \(x\in \mathbb{R}\). Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(g\left( x \right)=f\left( \left| {{x}^{3}}+3x \right|+2m-{{m}^{2}} \right)\) có không quá \(6\) điểm cực trị?

Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(\int\limits_{0}^{1}{f\left( 1-2x \right)}\,dx=\frac{1}{3}.\) Tích phân \(\int\limits_{-1}^{1}{f\left( x \right)}\,dx\) bằng

Trong không gian \(Oxyz\), cho tam giác \(ABC\) có \(A\left( -1;2;0 \right)\), \(B\left( 3;1;1 \right)\) và \(C\left( 1;6;5 \right)\). Trọng tâm tam giác \(ABC\) có tọa độ là

Trong không gian \(Oxyz\), cho đường thẳng \(\Delta :\frac{x-5}{3}=\frac{y}{2}=\frac{z+25}{-2}\) và điểm \(M\left( 2;3;-1 \right)\). Mặt phẳng \(\left( P \right):2x+by+cz+d=0\) chứa đường thẳng \(\Delta \). Khi khoảng cách từ \(M\) đến \(\left( P \right)\) lớn nhất, giá trị của \(b+c+d\) bằng

Trong không gian \(Oxyz,\) mặt phẳng đi qua ba điểm \(A\left( 1;-2;1 \right),\,\,B\left( 4;-5;1 \right)\) và \(C\left( 2;0;2 \right)\) có phương trình là

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(AB=1\), cạnh bên \(SA=1\) và vuông góc với mặt phẳng đáy \(\left( ABCD \right)\). Kí hiệu \(M\) là điểm di động trên đoạn \(CD\) và \(N\) là điểm di động trên đoạn \(CB\)sao cho \(\widehat{MAN}=45{}^\circ \). Thể tích nhỏ nhất của khối chóp \(S.AMN\) là

Cho các số thực dương \(a,\,\,b\) thỏa mãn \({{a}^{4}}{{b}^{3}}=1.\) Giá trị của \({{\log }_{a}}\frac{{{a}^{2}}}{{{b}^{3}}}\) bằng

Trong không gian với hệ trục tọa độ \(Oxyz\), cho điểm \(A\left( 2\ ;\ 1\ ;\ 3 \right)\) và mặt phẳng \(\left( P \right):x+my+\left( 2m+1 \right)z-m-2=0\), với \(m\) là tham số. Gọi \(H\left( a;b;c \right)\) là hình chiếu vuông góc của điểm \(A\) trên \(\left( P \right)\). Khi khoảng cách từ điểm \(A\) đến \(\left( P \right)\) lớn nhất; tính \(a+b\).

Có bao nhiêu số tự nhiên gồm 2 chữ số phân biệt?

Xét các số thực \(a\) thay đổi thỏa mãn \(\left| a \right|\le 2\) và \({{z}_{1}}\), \({{z}_{2}}\) là các nghiệm phức của phương trình \({{z}^{2}}-az+1=0\). Gọi \(A\left( \frac{7}{2};2 \right)\) và \(M\), \(N\) lần lượt là điểm biểu diễn số phức \({{z}_{1}}\) và \({{z}_{2}}\). Giá trị lớn nhất của diện tích tam giác \(AMN\) bằng

Đạo hàm của hàm số \(f\left( x \right)={{3}^{2-x}}\)

Cho hàm số bậc bốn \(y=\,f(x)\) có đồ thị như hình vẽ bên.

Số nghiệm thực của phương trình \(f(x)=\,1\) là

Cho \(\int\limits_{0}^{2}{f\left( x \right)dx}=4\); \(\int\limits_{0}^{2}{g\left( x \right)dx}=1\). Tích phân \(\int\limits_{0}^{2}{\left[ f\left( x \right)-2g\left( x \right) \right]dx}\) bằng