Trắc nghiệm Phép đối xứng trục Toán Lớp 11
-
Câu 1:
Trong mặt phẳng tọa độ Oxy cho tam giác ABC với \(A(0 ; 4), \quad B(-2 ; 3), C(6 ;-4)\) Gọi G là trọng tâm tam giác ABC và a là đường phân giác của góc phần tư thứ nhất. Phép đối xứng trục \(Đ_a\) biến G thành G ' có tọa độ là:
A. \(\left(\frac{4}{3} ; 1\right)\)
B. \(\left(-\frac{4}{3} ; 1\right)\)
C. \(\left(1 ; \frac{4}{3}\right)\)
D. \(\left(-1 ;-\frac{4}{3}\right)\)
-
Câu 2:
Trong mặt phẳng tọa độ Oxy , gọi d là đường phân giác của góc phần tư thứ hai. Phép đối xứng trục \(Đ_{d} \) biến điểm P(5;-2) thành điểm P ' có tọa độ là:
A. \((5 ; 2)\)
B. \((-5 ; 2)\)
C. \((2 ;-5)\)
D. \((-2 ; 5)\)
-
Câu 3:
Trong mặt phẳng tọa độ Oxy cho đường thẳng ∆ có phương trình \(2 x-y+1=0\) và điểm A(3;2 ). Trong các điểm dưới đây, điểm nào là điểm đối xứng của A qua đường thẳng ∆?
A. \(A_{1}^{\prime}(-1 ; 4)\)
B. \(A_{2}^{\prime}(-2 ; 5)\)
C. \(A_{3}^{\prime}(6 ;-3)\)
D. \(A_{4}^{\prime}(1 ; 6)\)
-
Câu 4:
Trong mặt phẳng tọa độ Oxy cho điểm M (2;3). Hỏi trong bốn điểm sau điểm nào là ảnh của M qua phép đối xứng đường thẳng \(d: x-y=0 ?\)
A. \(M_{1}^{\prime}(3 ; 2)\)
B. \(M_{2}^{\prime}(2 ;-3)\)
C. \(M_{3}^{\prime}(3 ;-2)\)
D. \(M_{4}^{\prime}(-2 ; 3)\)
-
Câu 5:
Trong mặt phẳng tọa độ Oxy , gọi a là đường thẳng có phương trình \(x+2=0\). Phép đối xứng trục \(Đ_{a} \) biến điểm M (4;-3) thành M ' có tọa độ là:
A. (-6 ;-3)
B. (-8 ;-3)
C. (8 ; 3)
D. (6 ; 3)
-
Câu 6:
rong mặt phẳng tọa độ Oxy cho tam giác ABC với \(A(1 ; 5), \quad B(-1 ; 2), C(6 ;-4\) Gọi G là trọng tâm của tam giác ABC. Phép đối xứng trục \(Đ_{O y}\) biến điểm G thành điểm G' có tọa độ là:
A. (-2 ;-1)
B. (2 ;-4)
C. (0 ;-3)
D. (-2 ; 1)
-
Câu 7:
Trong mặt phẳng tọa độ Oxy qua phép đối xứng trục Oy , điểm A(3;5) biến thành điểm nào trong các điểm sau?
A. \(A_{1}^{\prime}(3 ; 5)\)
B. \(A_{2}^{\prime}(-3 ; 5)\)
C. \(A_{3}^{\prime}(3 ;-5)\)
D. \(A_{4}^{\prime}(-3 ;-5)\)
-
Câu 8:
Trong mặt phẳng tọa độ Oxy cho điểm M (2;3). Hỏi trong bốn điểm sau điểm nào là ảnh của M qua phép đối xứng trục Ox ?
A. \(M_{1}^{\prime}(3 ; 2)\)
B. \(M_{2}^{\prime}(2 ;-3)\)
C. \(M_{3}^{\prime}(3 ;-2)\)
D. \(M_{4}^{\prime}(-2 ; 3)\)
-
Câu 9:
Mệnh đề nào sau đây là sai?
A. Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.
B. Phép đối xứng trục biến một đường thẳng thành một đường thẳng song song hoặc trùng với đường thẳng đã cho.
C. Phép đối xứng trục biến tam giác thành tam giác bằng tam giác đã cho.
D. Phép đối xứng trục biến đường tròn thành đường tròn bằng đường tròn đã cho.
-
Câu 10:
Cho hai điểm A, B cùng phía với đường thẳng d. gọi A’, B’ lần lượt là hình chiếu của A, B trên đường thẳng d. Tìm vị trí điểm C trên d để chu vi tam giác ABC nhỏ nhất.
A. C trùng với A’
B. C trùng với B’
C. C là trung điểm của A’B’
D. Vị trí khác
-
Câu 11:
Đồ thị của hàm số \(y=\cos x\)có bao nhiêu trục đối xứng?
A. 0
B. 1
C. 2
D. Vô số.
-
Câu 12:
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x-2y+2=0 và đường thằng l có phương trình : x - y + 1 = 0. Phép đối xứng trục l biến d thành d’ có phương trình
A. 2x - y - 1 = 0
B. 2x - y + 1 = 0
C. 2x + y + 1 = 0
D. 2x + y - 1 = 0
-
Câu 13:
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x - 8y + 11 = 0. Phép đối xứng trục Oy biến d thành d’ có phương trình:
A. 2x + 8y - 11 = 0
B. 2x - 8y + 11 = 0
C. 2x + 8y + 11 = 0
D. 2x - 8y - 11 = 0
-
Câu 14:
Trong mặt phẳng Oxy cho parabol (P) có phương trình y = 4x2 − 7x + 3. Phép đối xứng trục Oy biến (P) thành (P’) có phương trình:
A. y = 4x2 + 7x − 3
B. y = 4x2 + 7x + 3
C. y = −4x2 + 7x − 3
D. y = −4x2 − 7x + 3
-
Câu 15:
Trên tia phân giác ngoài Cx của góc C của tam giác ABC lấy điểm M không trùng với C. Tìm mệnh đề đúng nhất:
A. MA + MB < CA + CB
B. MA + MB > CA + CB
C. MA + MB ≥ CA + CB
D. MA + MB ≤ CA + CB
-
Câu 16:
Cho hai đường thẳng song song a và b , một đường thẳng c vuông góc với chúng. Có bao nhiêu phép đối xứng trục biến mỗi đường thẳng đó thành chính nó?
A. 0
B. 1
C. 2
D. Vô số.
-
Câu 17:
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: \({x^2}\; + \;{y^2}\; - \;4x\; + \;5y\; + \;1\; = \;0\). Phép đối xứng trục Oy biến (C) thành (C’) có phương trình:
A. \({x^2}\; + \;{y^2}\; - \;4x\;-\;5y\; + \;1\; = \;0\)
B. \({x^2}\; + \;{y^2}\; +\;4x\;+\;5y\; + \;1\; = \;0\)
C. \({x^2}\; + \;{y^2}\; - \;4x\;+\;5y\; + \;1\; = \;0\)
D. \({x^2}\; + \;{y^2}\; + \;4x\;-\;5y\; + \;1\; = \;0\)
-
Câu 18:
Trong mặt phẳng Oxy cho parabol (P) có phương trình: \(y\; = \;6{x^2}\; - \;3x\; + \;13\). Phép đối xứng trục Ox biến (P) thành (P’) có phương trình:
A. y = 6x2 + 3x − 13
B. y = 6x2 − 3x − 13
C. y = −6x2 + 3x − 1
D. y = −6x2 − 3x − 13
-
Câu 19:
Cho hai đường thẳng song song d và d ' . Có bao nhiêu phép đối xứng trục biến đường thẳng d thành đường thẳng d '?
A. 0
B. 1
C. 2
D. Vô số.
-
Câu 20:
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Phép đối xứng trục Oy biến d thành d’ có phương trình
A. 3x + 3y - 2 = 0
B. x - y + 2 = 0
C. x + y + 2 = 0
D. x + y - 3 = 0
-
Câu 21:
Cho hai đường thẳng song song d và d ' . Có bao nhiêu phép đối xứng trục biến mỗi đường thẳng thành chính nó ?
A. 0
B. 1
C. 2
D. Vô số.
-
Câu 22:
Có bao nhiêu phép đối xứng trục biến một hình chữ nhật thành chính nó?
A. không có
B. một
C. hai
D. vô số
-
Câu 23:
Trong mặt phẳng cho hai đường thẳng a và b tạo với nhau góc 60o. Có bao nhiêu phép đối xứng trục biến a thành b.
A. một
B. hai
C. ba
D. bốn
-
Câu 24:
Cho hai đường thẳng a và b cắt nhau và góc ở giữa chúng bằng 600 . Có bao nhiêu phép đối xứng trục biến a thành a và biến b thành b ?
A. 0
B. 1
C. 2
D. Vô số.
-
Câu 25:
Trong mặt phẳng, cho hình thang cân ABCD có AD = BC. Tìm mệnh đề đúng:
D. có phép đối xứng trục biến DA thành CB nên DA = CB
A. có phép đối xứng trục biến \(\overrightarrow {AD}\) thành \(\overrightarrow {BC}\) nên \(\overrightarrow {AD} \; = \;\overrightarrow {BC} \)
B. có phép đối xứng trục biến \(\overrightarrow {AC}\) thành \(\overrightarrow {BD}\) nên \(\overrightarrow {AC} \; = \;\overrightarrow {BD} \)
C. có phép đối xứng trục biến AB thành CD nên AB // CD
D. có phép đối xứng trục biến DA thành CB nên DA = CB
-
Câu 26:
Hình gồm hai đường thẳng d và d ' vuông góc với nhau có mấy trục đối xứng?
A. 0
B. 2
C. 4
D. Vô số
-
Câu 27:
Trong mặt phẳng, hình nào sau đây có trục đối xứng?
A. hình thang vuông
B. hình bình hành
C. hình tam giác vuông không cân
D. hình tam giác cân
-
Câu 28:
Cho hai đường thẳng vuông góc với nhau a và b . Có bao nhiêu phép đối xứng trục biến a thành a và biến b thành b ?
A. 0
B. 1
C. 2
D. Vô số.
-
Câu 29:
Trong mặt phẳng, hình vuông có mấy trục đối xứng?
A. một
B. hai
C. ba
D. bốn
-
Câu 30:
Trong các mệnh đề sau mệnh đề nào đúng?
A. Tam giác đều có vô số trục đối xứng
B. Một hình có vô số trục đối xứng thì hình đó phải là đường tròn
C. Hình gồm hai đường thẳng vuông góc có vô số trục đối xứng
D. Hình tròn có vô số trục đối xứng
-
Câu 31:
Cho hai đường thẳng cắt nhau d và d ' . Có bao nhiêu phép đối xứng trục biến d thành d ' ?
A. 0
B. 1
C. 2
D. Vô số.
-
Câu 32:
Trong mặt phẳng Oxy cho điểm M(2;3). Điểm M là ảnh của điểm nào trong bốn điểm sau qua phép đối xứng trục Oy?
A. A(3;2)
B. B(2; -3)
C. C(3;-2)
D. D(-2;3)
-
Câu 33:
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: (x − 3)2 + (y − 1)2 = 6. Phép đối xứng trục Oy biến (C) thành (C’) có phương trình
A. (x + 3)2 + (y − 1)2 = 36
B. (x + 3)2 + (y − 1)2 = 6
C. (x − 3)2 + (y + 1)2 = 36
D. (x + 3)2 + (y + 1)2 = 6
-
Câu 34:
Trong mặt phẳng Oxy cho đường thẳng d có phương trình : x - 2y + 4 = 0. Phép đối xứng trục Ox biến d thành d’ có phương trình:
A. x - 2y + 4 = 0
B. x + 2y + 4 = 0
C. 2x + y + 2 = 0
D. 2x - y + 4 = 0
-
Câu 35:
Trong mặt phẳng Oxy cho điểm M(-1;3). Phép đối xứng trục Ox biến M thành M’ thì tọa độ M’ là:
A. M’(-1;3)
B. M’(1;3)
C. M’(-1;-3)
D. M’(1;-3)
-
Câu 36:
Cho hình vuông ABCD tâm I. gọi E, F, G, H lần lượt là trung điểm của các cạnh DA, AB, BC, CD. Phép đối xứng trục AC biến:
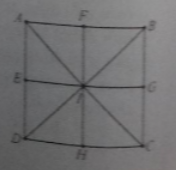
A. ∆IED thành ∆IGC
B. ∆IFB thành ∆IGB
C. ∆IBG thành ∆IDH
D. ∆IGC thành ∆IFA
-
Câu 37:
Có bao nhiêu phép đối xứng trục biến một đường thẳng d cho trước thành chính nó?
A. Không có phép nào.
B. Có một phép duy nhất.
C. Chỉ có hai phép.
D. Có vô số phép
-
Câu 38:
Mệnh đề nào sau đây sai?
A. Hình gồm hai đường tròn không bằng nhau có trục đối xứng.
B. Hình gồm một đường tròn và một đoạn thẳng tùy ý có trục đối xứng.
C. Hình gồm một đường tròn và một đường thẳng tùy ý có trục đối xứng.
D. Hình gồm một tam giác cân và đường tròn ngoại tiếp tam giác đó có trục đối xứng
-
Câu 39:
Cho ba đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình H . Hỏi H có mấy trục đối xứng?
A. 0
B. 1
C. 2
D. 3
-
Câu 40:
Hình gồm hai đường tròn có tâm và bán kính khác nhau có bao nhiêu trục đối xứng?
A. 0
B. 1
C. 2
D. Vô số.
-
Câu 41:
Xem các chữ cái in hoa A, B, C, D, X, Y như những hình. Khẳng định nào sau đây đúng?
A. Hình có một trục đối xứng là: A, Y. Các hình khác không có trục đối xứng.
B. Hình có một trục đối xứng: A, B, C, D, Y. Hình có hai trục đối xứng: X.
C. Hình có một trục đối xứng: A, B. Hình có hai trục đối xứng: D, X.
D. Hình có một trục đối xứng: C, D, Y. Hình có hai trục đối xứng: X. Các hình khác không có trục đối xứng.
-
Câu 42:
Trong các hình dưới đây, hình nào có nhiều trục đối xứng nhất?
A. Đoạn thẳng.
B. Đường tròn.
C. Tam giác đều.
D. Hình vuông.
-
Câu 43:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Tam giác có trục đối xứng.
B. Tứ giác có trục đối xứng.
C. Hình thang có trục đối xứng.
D. Hình thang cân có trục đối xứng.
-
Câu 44:
Hình nào sau đây có trục đối xứng:
A. Tứ giác bất kì
B. Tam giác cân
C. Tam giác bất kì
D. Hình bình hành
-
Câu 45:
Trong các hình sau đây, hình nào có bốn trục đối xứng?
A. Hình bình hành.
B. Hình chữ nhật.
C. Hình thoi.
D. Hình vuông
-
Câu 46:
Tam giác đều có bao nhiêu trục đối xứng?
A. 0
B. 1
C. 3
D. Vô số.
-
Câu 47:
Trong mặt phẳng tọa độ Oxy, cho biết A(3,5) Tìm tọa độ A’ là ảnh của điểm A qua phép đối xứng trục Ox.
A. A'(-3;-5)
B. A'(5;3)
C. A'(-3;5)
D. A'(3;-5)
-
Câu 48:
Cho tam giác đều ABC như hình vẽ. tam giác OFB biến thành tam giác ODC qua phép biến hình nào sau đây?
A. phép đối xứng tâm I
B. liên tiếp phép đối xứng trục AD và phép đối xứng trục CF
C. liên tiếp phép đối xứng tâm O và phép đối xứng trục OC
D. phép quay tâm A góc quay 60o
-
Câu 49:
Trong mặt phẳng Oxy, thực hiện liên tiếp ghép đối xứng trục Oy và ghép quay tâm O góc quay 90o biến điểm M(1;1) thành điểm M’’. tọa độ M’’ là:
A. (-1;1)
B. (-1;-1)
C. (1;-1)
D. \(\left( { - \sqrt 2 ; - \sqrt 2 } \right)\)
