ADMICRO
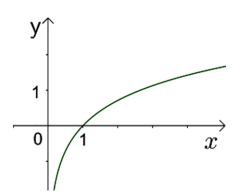
Tìm các khoảng đồng biến của hàm số x > 0
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ZUNIA12
Lời giải:
Báo sai
y' = 0 ⇔ ⇔ x >
⇒ Khoảng đồng biến của hàm số là
ZUNIA9
AANETWORK