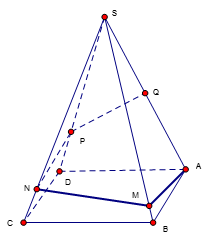
Cho hình chóp S.ABCD có đáy là hình chữ nhật, \(AB = a,{\rm{ }}AC = 2a,{\rm{ }}SA\) vuông góc với mặt phẳng (ABCD). SC tạo với mặt phẳng (SAB) một góc 30o. Gọi M là một điểm trên cạnh AB sao cho \(BM = 3MA.\) Khoảng cách từ điểm A đến mặt phẳng (SCM) là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Đặc điểm của hình: SC tạo với mặt phẳng (SAB) góc \(\widehat {CSB} = {30^ \circ }.\)
\(\begin{array}{l} BC = \sqrt 3 a\\ SB = BC.\tan {30^0} = a\\ MC = \sqrt {{{\left( {\frac{{3a}}{4}} \right)}^2} + 3{a^2}} = \frac{{\sqrt {57} }}{4}a\\ MA = \frac{a}{4};AC = 2a;AS = 2\sqrt 2 a\\ AK = \frac{{2{S_{AMC}}}}{{MC}} = \frac{{\sqrt {19} }}{{19}}a \end{array}\)
Xác định khoảng cách: \(d\left( {A,\left( {SBC} \right)} \right) = AH\)
Tính \(\frac{1}{{A{H^2}}} = \frac{1}{{A{K^2}}} + \frac{1}{{A{S^2}}} = \frac{1}{{{{\left( {\frac{{\sqrt {19} }}{{19}}a} \right)}^2}}} + \frac{1}{{{{\left( {2\sqrt 2 a} \right)}^2}}} = \frac{{153}}{{8{a^2}}}\)
Vậy \(d\left( {A,\left( {SBC} \right)} \right) = AH = \frac{{2\sqrt {34} }}{{51}}\)
Câu hỏi liên quan
-
Cho hình chóp S.ABCD có \(V = {a^3}\sqrt 3 \). Đáy là hình vuông cạnh a, hãy tính khoảng cách từ S đến mặt phẳng ABCD.
-
Cho hình chóp \(SABC{\rm{D}}\) có \(SA \bot \left( {ABC{\rm{D}}} \right)\), đáy \(ABC{\rm{D}}\) là hình chữ nhật. Biết \(A{\rm{D}} = 2{\rm{a}},SA = a\). Khoảng cách từ A đến \(\left( {SC{\rm{D}}} \right)\) bằng:
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa hai mặt phẳng (ACD') và (BA'C') bằng
-
Cho hình chóp tứ giác đều có cạnh đáy bằng a và góc hợp bởi một cạnh bên và mặt đáy bằng alpha . Khoảng cách từ tâm của đáy đến một cạnh bên bằng
-
Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh bằng \(\sqrt{2}a\). Tam giác SAD cân tại S và mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng \(\frac{4}{3}{{a}^{3}}\). Khoảng cách h từ B đến mặt phẳng (SCD) là:
-
Tính khoảng cách giữa hai cạnh đối trong một tứ diện đều cạnh a.
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên). Khoảng cách từ A đến mặt phẳng \(\left( {SBD} \right)\) bằng
.png)
-
Cho lăng trụ đứng \(ABC.ABC\) có đáy ABC là tam giác vuông tại B với \(AB=4a,BC=3\text{a},AC=5\text{a}\), cạnh bên \(BB'=9\text{a}\). Gọi M là điểm thuộc BB’ sao cho BB' = 3B'M. Khoảng cách giữa B’C và AM là
-
Cho hình chóp SABC, \(\Delta SAB\) đều cạnh a nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ C đến mặt phẳng \(\left( {SAB} \right)\) biết \(V = \frac{{{a^3}\sqrt 3 }}{6}\).
-
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD = 2a. Biết \(SA = \sqrt3 a \) và SA vuông góc (ABCD). Gọi H là hình chiếu vuông góc của A trên (SBC) Tính khoảng cách d từ H đến mặt phẳng SCD
-
Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC) và SA = 3a. Diện tích tam giác ABC bằng 2a2. Khoảng cách từ S đến BC bằng bao nhiêu?
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa BB' và AC bằng
-
Cho hình chóp O.ABC có đường cao \(OH = \frac{{2a}}{{\sqrt 3 }}\). Gọi M và N lần lượt là trung điểm của OA và OB. Tính khoảng cách giữa đường thẳng MN và (ABC).
-
Cho lăng trụ \(ABC.ABC\) các mặt đều là hình vuông cạnh a. Gọi D là trung điểm của cạnh \(BC.\) Tính khoảng cách giữa hai đường thẳng A’B’ và DC’ theo a
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a. Khoảng cách giữa hai đường thẳng SB và CD nhận giá trị nào trong các giá trị sau?
-
Cho tứ diện ABCD, \(DA \bot \left( {ABC} \right)\) và \(\widehat {ABC} = 90^\circ ,BA = a\sqrt 3 ,BC = a\). Tính khoảng cách từ C đến mặt phẳng \(\left( {DAB} \right)\).
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với đáy và \(SA = a\sqrt 3 \). Biết diện tích tam giác SAB là \(\frac{{{a^2}\sqrt 3 }}{2}\). Khoảng cách từ điểm B đến \(\left( {SAC} \right)\) là:
-
Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a, tam giác SBA vuông tại B, tam giác SAC vuông tại C. Biết góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {ABC} \right)\) bằng \(60^\circ \). Tính khoảng cách giữa SC và AB theo a.
-
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \(\widehat{ABC}={{30}^{0}}\), tam giác SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách h từ điểm C đến mặt phẳng (SAB).
-
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I với \(AB = 2a\sqrt 3 ;BC = 2a\). Biết chân đường cao H hạ từ đỉnh S xuống đáy ABCD trùng với trung điểm đoạn DI và SB hợp với mặt phẳng đáy (ABCD) một góc 60o. Khoảng cách từ D đến (SBC) tính theo a bằng
