Cho khối nón có đỉnh S, chiều cao bằng 8 và thể tích bằng \(\frac{{800\pi }}{3}\). Gọi A và B là hai điểm thuộc đường tròn đáy sao cho AB = 12, khoảng cách từ tâm của đường tròn đáy đến mặt phẳng \(\left( {SAB} \right)\) bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
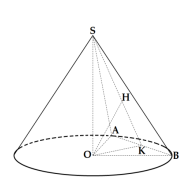
Báo saiGọi O , R lần lượt là tâm và bán kính đáy của khối nón, K , H lần lượt là hình chiếu của
O lên AB , SK . Khi đó khoảng cách từ tâm của đường tròn đáy đến mặt phẳng (SAB)
bằng OH .
\(V = \frac{1}{3}\pi {R^2}h \Rightarrow R = \sqrt {\frac{{3V}}{{\pi h}}} = 10\).
Trong tam giác vuông OBK có:
\(\begin{array}{l}
OK = \sqrt {O{B^2} - B{K^2}} \\
= \sqrt {{R^2} - {{\left( {\frac{{AB}}{2}} \right)}^2}} \\
= \sqrt {{{10}^2} - {6^2}} = 8
\end{array}\)
Trong tam giác vuông SOK có:
\(\begin{array}{l}
\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{K^2}}}\\
= \frac{1}{{{8^2}}} + \frac{1}{{{8^2}}}\\
= \frac{2}{{{8^2}}}\\
\Rightarrow OH = 4\sqrt 2
\end{array}\)
Vậy khoảng cách từ tâm của đường tròn đáy đến mặt phẳng \(\left( {SAB} \right)\) bằng \(4\sqrt 2 \).
Đáp án C