Cho hình chóp đều \(S.ABCD\) có chiều cao \(a,AC = 2a\) (tham khảo hình bên).
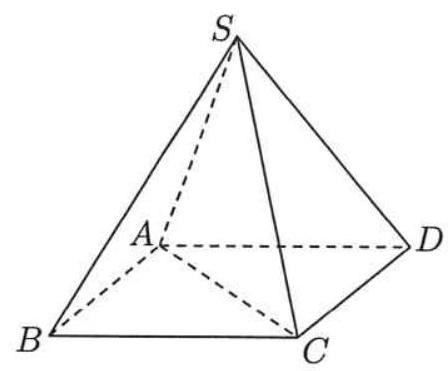
Khoảng cách từ B đến mặt phẳng \(\left( {SCD} \right)\) bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi O = AC ∩ BD, H là trung điểm CD . Trong (SOH ) , kẻ OI SH ⊥ SH.
Có \(\left\{ \begin{array}{l} CD \bot SO\\ CD \bot SH \end{array} \right. \\ \Rightarrow CD \bot \left( {SOH} \right) \\ \Rightarrow CD \bot OI\)
Mà \(OI \bot SH\) nên
\(\begin{array}{l} OI \bot \left( {SCD} \right)\\ \Rightarrow d\left( {O;\left( {SCD} \right)} \right) = OI = \frac{{SO.OH}}{{\sqrt {S{O^2} + O{H^2}} }} \end{array}\)
Vì O là trung điểm BD nên
\(\begin{array}{l} d\left( {B;\left( {SCD} \right)} \right) = 2d\left( {O;\left( {SCD} \right)} \right)\\ = 2OI\\ = \frac{{2SO.OH}}{{\sqrt {S{O^2} + O{H^2}} }} \end{array}\)
Có \(AD=AC\sin45^0=a\sqrt{2}\)
\(OH = \frac{{a\sqrt 2 }}{2} \Rightarrow d\left( {B,\left( {SCD} \right)} \right) = \frac{{2a\sqrt 3 }}{3}\)
Đáp án C
\(\frac{{2\sqrt 3 }}{3}a\)
Câu hỏi liên quan
-
Cho hàm số \(f\left( x \right) = {\text{cos}}x + x\). Khẳng định nào dưới đây đúng?
-
Cho \(\smallint \frac{1}{x}{\text{d}}x = F\left( x \right) + C\). Khẳng định nào dưới đây đúng?
-
Trong không gian \(Oxyz\), góc giữa hai mặt phẳng \(\left( {Oxy} \right)\) và \(\left( {Oyz} \right)\) bằng
-
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x + 1}}{{3x - 1}}\) là đường thẳng có phương trình:
-
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Giá trị cực đại của hàm số đã cho là
-
Tích tất cả các nghiệm của phương trình \({\text{l}}{{\text{n}}^2}x + 2{\text{ln}}x - 3 = 0\) bằng
-
Cho mặt phẳng (P) tiếp xúc với mặt cầu \(S\left( {O;R} \right)\). Gọi d là khoảng cách từ O đến (P). Khẳng định nào dưới đây đúng?
-
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {0;0;10} \right)\) và \(B\left( {3;4;6} \right)\). Xét các điểm M thay đổi sao cho tam giác AOM không có góc tù và có diện tích bằng 15. Giá trị nhỏ nhất của độ dài đoạn thẳng MB thuộc khoảng nào dưới đây?
-
Cho tập hợp A có 15 phần tử. Số tập con gồm hai phần tử của A bằng
-
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {(x - 2)^2}\left( {1 - x} \right)\) với mọi \(x \in \mathbb{R}\). Hàm số đã cho đồng biến trên khoảng nào dưới đây?
-
Cho khối chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(A,AB = 2\), \(SA\) vuông góc với đáy và \(SA = 3\) (tham khảo hình bên). Thể tích khối chóp đã cho bằng?
-
Cho số phức \(z = 2 + 9i\), phần thực của số phức \({z^2}\) bằng
-
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và công bội \(q = \frac{1}{2}\). Giá trị của u3 bằng
-
Trên khoảng \(\left( {0; + \infty } \right)\), đạo hàm của hàm số \(y = {x^\pi }\) là:
-
Trên tập hợp số phức, xét phương trình \({z^2} - 2\left( {m + 1} \right)z + {m^2} = 0\) (
là tham số thực). Có bao nhiêu giá trị của m để phương trình đó có hai nghiệm phân biệt \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1}} \right| + \left| {{z_2}} \right| = 2\) ? -
Tập nghiệm của bất phương trình \({\text{log}}\left( {x - 2} \right) > 0\) là
-
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 1 = 0\). Tâm của \(\left( S \right)\) có tọa độ là
-
Một hộp chứa 15 quả cầu gồm 6 quả màu đỏ được đánh số từ 1 đến 6 và 9 quả màu xanh được đánh số từ 1 đến 9. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả khác màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng
-
Cho khối lăng trụ đứng \(ABC \cdot A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(B,AB = a\). Biết khoảng cách từ A đến mặt phẳng \(\left( {A'BC} \right)\) bằng \(\frac{{\sqrt 6 }}{3}a\), thể tích khối lăng trụ đã cho bằng
