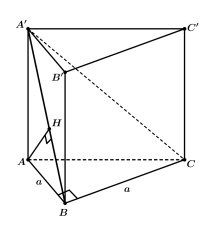
Cho khối lăng trụ đứng \(ABC \cdot A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(B,AB = a\). Biết khoảng cách từ A đến mặt phẳng \(\left( {A'BC} \right)\) bằng \(\frac{{\sqrt 6 }}{3}a\), thể tích khối lăng trụ đã cho bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Kẻ \(AH \bot A'B,H \in A'B\)
Vì \(\begin{array}{l} \left\{ \begin{array}{l} BC \bot AB\\ BC \bot AA' \end{array} \right. \Rightarrow BC \bot \left( {ABB'A'} \right)\\ \Rightarrow BC \bot AH \end{array}\)
Ta có \(\left\{ \begin{array}{l} BC \bot AH\\ AH \bot A'B \end{array} \right. \Rightarrow AH \bot \left( {A'BC} \right)\)
Do đó \(d\left( {A,\left( {A'BC} \right)} \right) = AH = \frac{{a\sqrt 6 }}{3}\)
Xét tam giác vuông AA'B vuông tại A , ta có
\(\begin{array}{l}
\frac{1}{{A{H^2}}} = \frac{1}{{AA{'^2}}} + \frac{1}{{A{B^2}}}\\
\Rightarrow \frac{1}{{AA{'^2}}} = \frac{1}{{A{H^2}}} - \frac{1}{{A{B^2}}}\\
\Rightarrow \frac{1}{{AA{'^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt 6 }}{3}} \right)}^2}}} - \frac{1}{{{a^2}}} = \frac{1}{{2{a^2}}}\\
\Rightarrow AA' = a\sqrt 2
\end{array}\).
Vậy
\({V_{ABC.A'B'C'}} = {S_{ABC}}.AA' = \frac{1}{2}a.a.a\sqrt 2 = \frac{{{a^3}\sqrt 2 }}{2}\)
Đáp án B
Thể tích khối lăng trụ đã cho bằng \(\frac{{\sqrt 2 }}{2}{a^3}\)
Câu hỏi liên quan
-
Trong không gian \(Oxyz\), cho hai điểm \(M\left( {1; - 1; - 1} \right)\) và \(N\left( {5;5;1} \right)\). Đường thẳng \(MN\) có phương trình là:
-
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và công bội \(q = \frac{1}{2}\). Giá trị của u3 bằng
-
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và thỏa mãn \(f\left( x \right) + xf'\left( x \right) = 4{x^3} + 4x + 2,\forall x \in \mathbb{R}\). Diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right)\) và \(y = f'\left( x \right)\) bằng
-
Có bao nhiêu cặp số nguyên \(\left( {x;y} \right)\) thỏa mãn \({\text{lo}}{{\text{g}}_3}\left( {{x^2} + {y^2} + x} \right) + {\text{lo}}{{\text{g}}_2}\left( {{x^2} + {y^2}} \right) \leqslant {\text{lo}}{{\text{g}}_3}x + {\text{lo}}{{\text{g}}_2}\left( {{x^2} + {y^2} + 24x} \right)?\)
-
Nếu \(\smallint _0^2f\left( x \right){\text{d}}x = 4\) thì \(\smallint _0^2\left[ {\frac{1}{2}f\left( x \right) - 2} \right]{\text{d}}x\) bằng
-
Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn \(\left| {z + 2i} \right| = 1\) là một đường tròn. Tâm của đường tròn đó có tọa độ là
-
Có bao nhiêu số nguyên \(x\) thỏa mãn \({\text{lo}}{{\text{g}}_3}\frac{{{x^2} - 16}}{{343}} < {\text{lo}}{{\text{g}}_7}\frac{{{x^2} - 16}}{{27}}\) ?
-
Cho hình nón có đường kính đáy \(2r\) và độ dài đường sinh \(l\). Diện tích xung quanh của hình nón đã cho bằng
-
Tập nghiệm của bất phương trình \({\text{log}}\left( {x - 2} \right) > 0\) là
-
Xét các số phức \(z\) thỏa mãn \(\left| {{z^2} - 3 - 4i} \right| = 2\left| z \right|\). Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(\left| z \right|\). Giá trị của \({M^2} + {m^2}\) bằng
-
Cho số phức \(z = 2 + 9i\), phần thực của số phức \({z^2}\) bằng
-
Cho khối lập phương có cạnh bằng 2. Thể tích của khối lập phương đã cho bằng
-
Cho mặt phẳng (P) tiếp xúc với mặt cầu \(S\left( {O;R} \right)\). Gọi d là khoảng cách từ O đến (P). Khẳng định nào dưới đây đúng?
-
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên.
Có bao nhiêu giá trị nguyên của tham số \( m \) để phương trình \(f\left( x \right) = m\) có ba nghiệm thực phân biệt?
-
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = - {x^4} + 6{x^2} + mx\) có ba điểm cực trị?
-
Trên khoảng \(\left( {0; + \infty } \right)\), đạo hàm của hàm số \(y = {\text{lo}}{{\text{g}}_3}x\) là:
-
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
-
Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right):x + y + z + 1 = 0\) có một vectơ pháp tuyến là:
-
Cho khối chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(A,AB = 2\), \(SA\) vuông góc với đáy và \(SA = 3\) (tham khảo hình bên). Thể tích khối chóp đã cho bằng?
-
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x + 1}}{{3x - 1}}\) là đường thẳng có phương trình:
