Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có mặt đáy \(ABC\) là tam giác vuông tại \(B\) có \(AB=a,\,AC=a\sqrt{3},\,{A}'B=2a\). Gọi \(M\) là trung điểm của cạnh \(AC\). Tính khoảng cách từ \(M\) đến \(\left( {A}'BC \right)\)
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn A
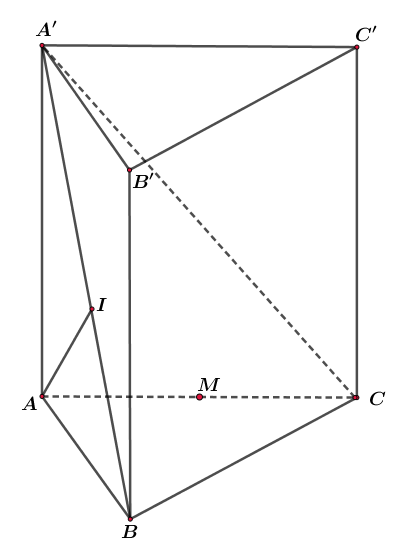
Gọi \(I\) là hình chiếu của \(A\) lên \(SB\).
Khi đó \(\left\{ \begin{align}
& BC\bot AB \\
& BC\bot A{A}' \\
\end{align} \right.\Rightarrow BC\bot \left( AB{A}' \right)\Rightarrow BC\bot AI\)
Ta có \(\left. \begin{align}
& AI\bot SB \\
& AI\bot BC \\
\end{align} \right\}\Rightarrow AI\bot \left( {A}'AB \right)\Rightarrow d\left( A,\,\left( {A}'AB \right) \right)=AI\)
\(A{{{A}'}^{2}}={A}'{{B}^{2}}-A{{B}^{2}}=4{{a}^{2}}-{{a}^{2}}=3{{a}^{2}}\Rightarrow A{A}'=a\sqrt{3}\)
Xét tam giác vuông \(AB{A}':\frac{1}{A{{I}^{2}}}=\frac{1}{A{{{{A}'}}^{2}}}+\frac{1}{A{{B}^{2}}}\Rightarrow AI=\frac{a\sqrt{3}.a}{\sqrt{3{{a}^{2}}+{{a}^{2}}}}=\frac{a\sqrt{3}}{2}\).
Ta có \(AM\cap \left( {A}'BC \right)=\left\{ C \right\}\Rightarrow \frac{d\left( M,\,\left( {A}'BC \right) \right)}{d\left( A,\,\left( {A}'BC \right) \right)}=\frac{CM}{CA}=\frac{1}{2}\)
\(\Rightarrow d\left( M,\,\left( {A}'BC \right) \right)=\frac{1}{2}.d\left( A,\,\left( {A}'BC \right) \right)=\frac{1}{2}.AI=\frac{a\sqrt{3}}{4}\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Nguyễn Bỉnh Khiêm