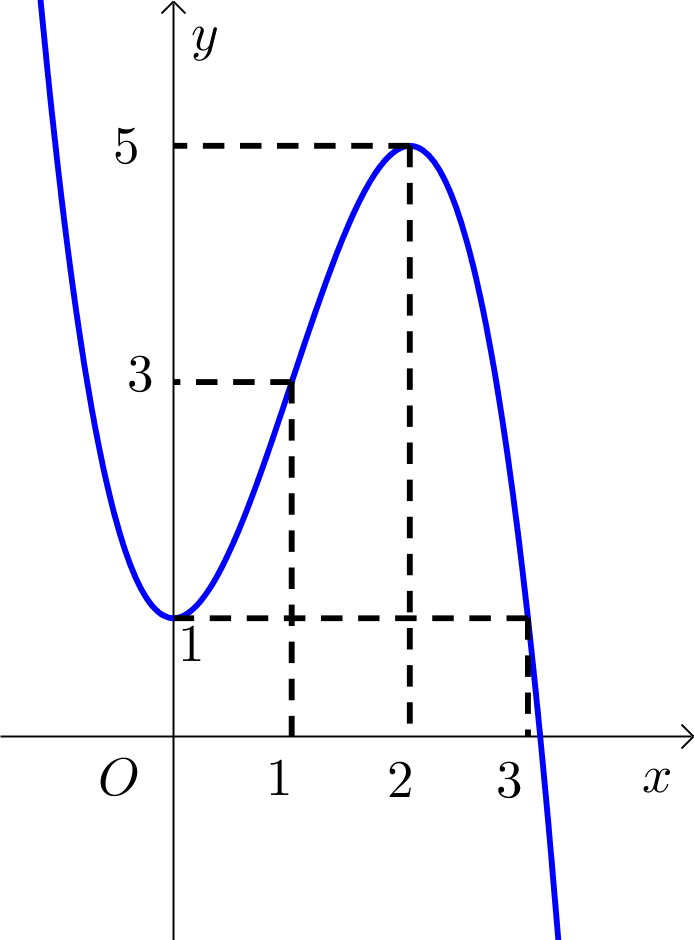
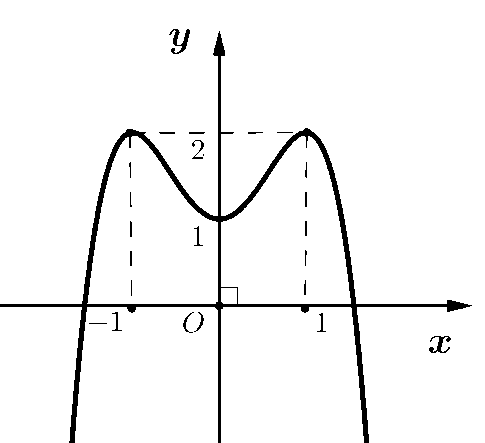
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:

Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho phương trình \(2f\left( \sin x-\cos x \right)=m-1\) có hai nghiệm phân biệt trên khoảng \(\left( -\frac{\pi }{4}\,;\,\frac{3\pi }{4} \right)\)?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(2f\left( \sin x-\cos x \right)=m-1\) \(\left( 1 \right)\).
Đặt \(t=\sin x-\cos x=\sqrt{2}\sin \left( x-\frac{\pi }{4} \right)\) \(\left( * \right)\).
Ta có: \(x\in \left( -\frac{\pi }{4}\,;\,\frac{3\pi }{4} \right)\Rightarrow x-\frac{\pi }{4}\in \left( -\frac{\pi }{2}\,;\,\frac{\pi }{2} \right)\Rightarrow \sin \left( x-\frac{\pi }{4} \right)\in \left( -1\,;\,1 \right)\Rightarrow t\in \left( -\sqrt{2}\,;\,\sqrt{2} \right)\).
Với mỗi \(t\in \left( -\sqrt{2}\,;\,\sqrt{2} \right)\) thì phương trình \(\left( * \right)\) có một nghiệm \(x\)tương ứng.
Khi đó phương trình \(\left( 1 \right)\)trở thành: \(\frac{m-1}{2}=f\left( t \right)\) \(\left( 2 \right)\).
\(\left( 1 \right)\) có hai nghiệm phân biệt trên khoảng \(\left( -\frac{\pi }{4}\,;\,\frac{3\pi }{4} \right)\)\(\Leftrightarrow \)\(\left( 2 \right)\) có hai nghiệm \(t\) phân biệt trên khoảng \(\left( -\sqrt{2}\,;\,\sqrt{2} \right)\)\(\Leftrightarrow -4<\frac{m-1}{2}<3\Leftrightarrow -7\)
Mà \(m\in \mathbb{Z}\)\(\Rightarrow m\in \left\{ -6\,;\,-5\,;\,...;\,5\,;\,6 \right\}\).
Vậy có \(13\) giá trị \(m\) nguyên thỏa đề bài.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Nguyễn Bỉnh Khiêm