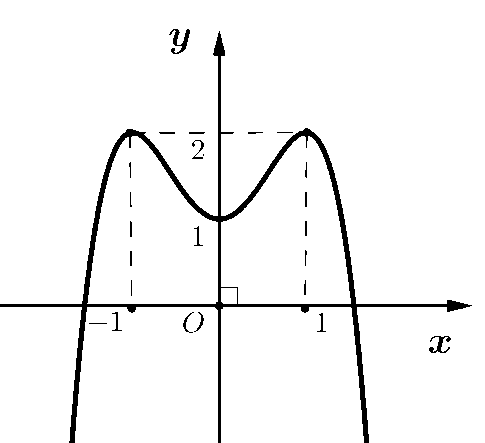
Cho hàm bậc ba \(f\left( x \right)\) có đồ thị hàm số như hình vẽ bên.
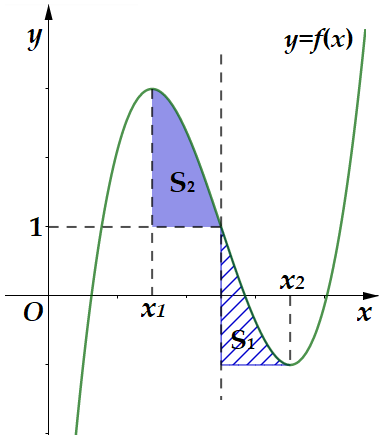
Biết hàm số \(f\left( x \right)\) đạt cực trị tại hai điểm \({{x}_{1}},{{x}_{2}}\) thỏa mãn \({{x}_{2}}={{x}_{1}}+2\) và \(f\left( {{x}_{1}} \right)+f\left( {{x}_{2}} \right)=2\). Gọi \({{S}_{1}},{{S}_{2}}\) là diện tích của hai hình phẳng được cho trong hình vẽ bên. Tính tỉ số \(\frac{{{S}_{1}}}{{{S}_{2}}}\)
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn B
Do \(f\left( x \right)\) đạt cực trị tại hai điểm \({{x}_{1}},{{x}_{2}}\)
\(\Rightarrow {f}'\left( x \right)=3a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)=3a\left( x-{{x}_{1}} \right)\left( x-{{x}_{1}}-2 \right)=3a{{\left( x-{{x}_{1}} \right)}^{2}}-6a\left( x-{{x}_{1}} \right),\,\,\,\left( a>0 \right)\)
\(\Rightarrow f\left( x \right)=a{{\left( x-{{x}_{1}} \right)}^{3}}-3a{{\left( x-{{x}_{1}} \right)}^{2}}+C\).
Ta có: \(f\left( {{x}_{1}} \right)=C\),\(f\left( {{x}_{2}} \right)=-4a+C\) và \(f\left( {{x}_{1}} \right)+f\left( {{x}_{2}} \right)=2\)\(\Rightarrow C=2a+1\)
\(\Rightarrow f\left( x \right)=a{{\left( x-{{x}_{1}} \right)}^{3}}-3a{{\left( x-{{x}_{1}} \right)}^{2}}+2a+1\).
Ta có: \({{S}_{2}}=\int\limits_{{{x}_{1}}}^{{{x}_{1}}+1}{\left| f\left( x \right)-1 \right|\text{d}x}=a\int\limits_{{{x}_{1}}}^{{{x}_{1}}+1}{\left[ {{\left( x-{{x}_{1}} \right)}^{3}}-3{{\left( x-{{x}_{1}} \right)}^{2}}+2 \right]\text{d}x}=a\int\limits_{0}^{1}{\left( {{t}^{3}}-3{{t}^{2}}+2 \right)\text{d}t}=\frac{5a}{4}\)
Do tính chất đối xứng qua điểm uốn của hàm bậc ba nên ta có được:
\(\frac{{{S}_{1}}}{{{S}_{2}}}=\frac{\left( f\left( {{x}_{1}} \right)-1 \right)-{{S}_{2}}}{{{S}_{2}}}=\frac{2a}{\frac{5a}{4}}-1=\frac{3}{5}\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Nguyễn Bỉnh Khiêm
Câu hỏi liên quan
-
Trong không gian với hệ tọa độ \(\text{O}xyz\), cho các điểm \(A\left( 1;0;0 \right)\), \(B\left( 0;2;0 \right)\),\(C\left( 0;0;4 \right)\).Viết phương trình đường thẳng \(\Delta \) đi qua trực tâm \(H\) của tam giác \(\Delta ABC\) và vuông góc với mặt phẳng \(\left( ABC \right)\).
-
Cho hàm đa thức bậc bốn \(y=f(x)\) có đồ thị như hình bên dưới.
Khẳng định nào đúng?
-
Xét các số phức \(\text{w}\), \(z\) thỏa mãn \(\left| \text{w}+i \right|=\frac{3\sqrt{5}}{5}\) và \(5w=\left( 2+i \right)\left( z-4 \right)\). Tìm giá trị lớn nhất của biểu thức \(P=\left| z-2i \right|+\left| z-6-2i \right|\).
-
Tập xác định của hàm số \(y={{({{x}^{3}}+27)}^{\frac{\pi }{2}}}\) là
-
Trong không gian với hệ trục tọa độ \(Oxyz\), từ điểm \(A\left( 1;1;0 \right)\) ta kẻ các tiếp tuyến đến mặt cầu \(\left( S \right)\) có tâm \(I\left( -1;1;1 \right)\) và bán kính \(R=1\). Gọi \(M\left( a;b;c \right)\) là một trong các tiếp điểm ứng với các tiếp tuyến trên. Tìm giá trị lớn nhất của biểu thức \(T=\left| 2a-b+2c \right|\).
-
Tìm họ các nguyên hàm của hàm số \(y={{e}^{x}}+2x\).
-
Phương trình \({{z}^{2}}+az+b=0;(a,b\in \mathbb{R})\)có nghiệm phức là \(3+4i\). Giá trị của \(a+b\)bằng:
-
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho phương trình \(2f\left( \sin x-\cos x \right)=m-1\) có hai nghiệm phân biệt trên khoảng \(\left( -\frac{\pi }{4}\,;\,\frac{3\pi }{4} \right)\)?
-
Trong không gian \(Oxyz\), cho đường thẳng \(d\) có phương trình \(d:\,\left\{ \begin{align}
& x=-1+t \\
& y=2-3t \\
& z=t \\
\end{align} \right.\) và điểm \(A\left( 2;\,3;\,1 \right).\)Mặt phẳng \(\left( P \right)\) đi qua điểm \(A\), vuông góc với đường thẳng \(d\) có phương trình là
-
Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có bốn đỉnh \(A,\,B,\,C,\,D\) và hai đường parabol có các đỉnh lần lượt là \(E,\,F\) (phần tô đậm của hình vẽ bên). Hai đường parabol có cùng trục đối xứng \(AB\), đối xứng nhau qua trục \(CD\), hai parabol cắt elip tại các điểm \(M,\,N,\,P,\,Q\). Biết \(AB=8\,m,\,CD=6\,m, \) \(MN=PQ=3\sqrt{3}\,m,\,EF=2\,m\). Chi phí để trồng hoa trên vườn là \(300.000\)đ/\({{m}^{2}}\). Hỏi số tiền trồng hoa cho cả vườn gần nhất với số tiền nào dưới đây?
-
Cho khối tứ diện \(ABCD\) có thể tích \(V\). Gọi \(V'\) là thể tích của khối tám mặt có các đỉnh là trung điểm các cạnh của khối đa diện \(ABCD\). Tính tỉ số \(\frac{V'}{V}\) bằng:
-
Cho số phức \(z=1-2i\). Phần ảo của số phức \(\overline{z}\) là?
-
Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(M(3;-1;1)\) trên trục \(Oz\) có tọa độ là
-
Giá trị cực tiểu của hàm số \(y=-{{x}^{3}}+3x+4\) là
-
Hàm số \(y=f\left( x \right)\) có đồ thị như hình vẽ bên. Giá trị của \(\int\limits_{-2}^{2}{f\left( x \right)dx}\) bằng
-
Gọi \(m,M\) lần lượt là giá trị nhỏ nhất, lớn nhất của hàm số \(y=x-\ln x\) trên đoạn \(\left[ \frac{1}{2};e \right]\). Giá trị của \(M-m\) là
-
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị \({f}'\left( x \right)\) như hình vẽ bên.
Bất phương trình \({{\log }_{5}}\left[ f\left( x \right)+m+2 \right]+f\left( x \right)>4-m\) đúng với mọi \(x\in \left( -1\,;\,4 \right)\)khi và chỉ khi
-
Tìm đường tiệm cận ngang của đồ thị hàm số \(y=\frac{3x-4}{x-1}\).
-
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):x+3y-2z+2=0\) và đường thẳng \(d:\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-4}{1}\). Đường thẳng qua \(A\left( 1;2;-1 \right)\) và cắt \(\left( P \right)\) và \(d\) lần lượt là tại \(B,\,\,C\left( a;b;c \right)\) sao cho \(C\) là trung điểm \(AB\). Giá trị biểu thức \(a+b+c\) bằng:
-
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=\frac{1}{3}{{x}^{3}}-m{{x}^{2}}-(2m-3)x-m+2\) luôn đồng biến trên \(\mathbb{R}?\)
