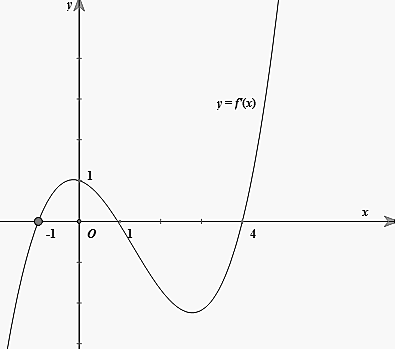
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị \({f}'\left( x \right)\) như hình vẽ bên.

Bất phương trình \({{\log }_{5}}\left[ f\left( x \right)+m+2 \right]+f\left( x \right)>4-m\) đúng với mọi \(x\in \left( -1\,;\,4 \right)\)khi và chỉ khi

A. \(m\ge 4-f\left( -1 \right)\).

B. \(m\ge 3-f\left( 1 \right)\).

C. \(m<4-f\left( -1 \right)\).

D. \(m\ge 3-f\left( 4 \right)\).

Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án

Chủ đề: Đề thi THPT QG

Môn: Toán

Lời giải:

Báo sai

Ta có, bất phương trình \({{\log }_{5}}\left[ f\left( x \right)+m+2 \right]+f\left( x \right)>4-m\).

\(\Leftrightarrow {{\log }_{5}}\left[ f\left( x \right)+m+2 \right]+f\left( x \right)+m+2>6\).

\(\Leftrightarrow {{\log }_{5}}\left[ f\left( x \right)+m+2 \right]+f\left( x \right)+m+2>{{\log }_{5}}\left( 5 \right)+5\).

Đặt: \(t=f\left( x \right)+m+2,\,\,\left( t>0 \right)\).

\(\Rightarrow {{\log }_{5}}\left( t \right)+t>{{\log }_{5}}\left( 5 \right)+5\).

Ta xét, hàm số \(f\left( t \right)={{\log }_{5}}\left( t \right)+t,\,\,\left( t>0 \right)\).

\(\Rightarrow {f}'\left( t \right)=\frac{1}{t\ln 5}+1>0,\,\,\forall t\in \left( 0\,\,;\,+\infty \right)\).

\(\Rightarrow f\left( t \right)={{\log }_{5}}\left( t \right)+t\) là hàm số đồng biến trên khoảng \(\left( 0\,\,;\,+\infty \right)\).

Ta có \(f\left( t \right)>f\left( 5 \right)\Rightarrow t>5\).

Vậy, bất phương trình \({{\log }_{5}}\left[ f\left( x \right)+m+2 \right]+f\left( x \right)>4-m\) đúng với mọi \(x\in \left( -1\,;\,4 \right)\) khi và chỉ khi \(f\left( x \right)+m+2>5,\,\,\forall x\in \left( -1\,;4 \right)\Leftrightarrow m>3-f\left( x \right),\,\forall x\in \left( -1\,;4 \right)\).

Dựa, vào đồ thị \({f}'\left( x \right)\) ta có:

\(\int_{-1}^{4}{{f}'\left( x \right)\text{d}x}<0\Leftrightarrow f\left( 4 \right)-f\left( -1 \right)<0\Leftrightarrow f\left( 4 \right)<f\left( -1 \right)\).

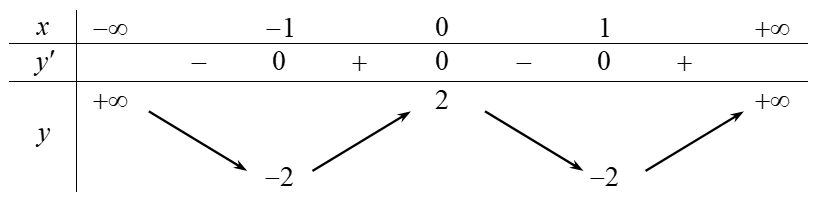
Mặt khác, dựa vào đồ thị hàm số \({f}'\left( x \right)\), ta có BBT vủa hàm số \(f\left( x \right)\) như sau

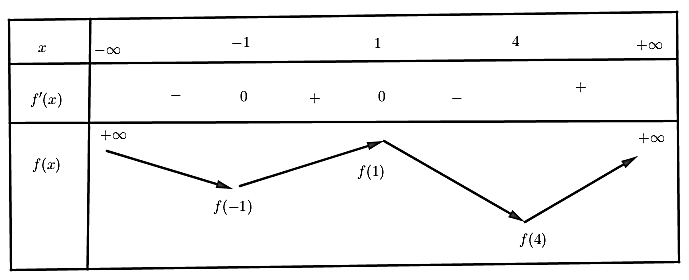
Vậy, hàm số \(3-f\left( x \right)\) có BBT như sau.

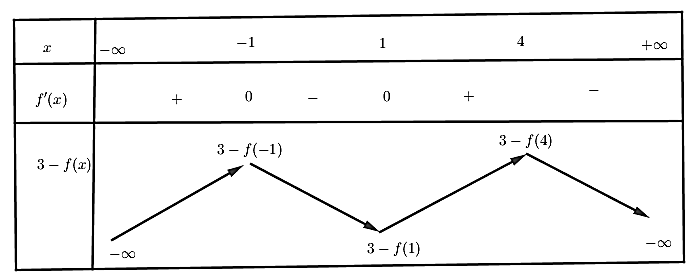
Vậy, \(m>3-f\left( x \right),\,\forall x\in \left( -1\,;4 \right)\Leftrightarrow \)\(m\ge 3-f\left( 4 \right).\)

Do đó, bất phương trình \({{\log }_{5}}\left[ f\left( x \right)+m+2 \right]+f\left( x \right)>4-m\) đúng với mọi \(x\in \left( -1\,;\,4 \right)\)khi và chỉ khi \(m\ge 3-f\left( 4 \right)\).

Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài