Xét các số phức \(\text{w}\), \(z\) thỏa mãn \(\left| \text{w}+i \right|=\frac{3\sqrt{5}}{5}\) và \(5w=\left( 2+i \right)\left( z-4 \right)\). Tìm giá trị lớn nhất của biểu thức \(P=\left| z-2i \right|+\left| z-6-2i \right|\).

A. \(7\).

B. \(2\sqrt{53}\).

C. \(2\sqrt{58}\).

D. \(4\sqrt{13}\).

Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án

Chủ đề: Đề thi THPT QG

Môn: Toán

Lời giải:

Báo sai

Cách 1.

Ta có: \(5w=\left( 2+i \right)\left( z-4 \right)\Leftrightarrow 5w+5i=\left( 2+i \right)\left( z-4 \right)+5i\)

\(\Rightarrow \left| 5w+5i \right|=\left| \left( 2+i \right)\left( z-4 \right)+5i \right|\Rightarrow 5\left| w+i \right|=\left| \left( 1+2i \right)\left( z-4+1+2i \right) \right|=\sqrt{5}\left| z-3+2i \right|\)

\(\Rightarrow 5.\frac{3\sqrt{5}}{5}=\sqrt{5}\left| z-3+2i \right|\Rightarrow \left| z-3+2i \right|=3\).

Ta có:

\({{\left| z+{{z}_{1}} \right|}^{2}}+{{\left| z-{{z}_{1}} \right|}^{2}}=2\left( {{\left| z \right|}^{2}}+{{\left| {{z}_{1}} \right|}^{2}} \right);\,\,\forall z,\,{{z}_{1}}\). (1)

\({{\left| z \right|}^{2}}+{{\left| {{z}_{1}} \right|}^{2}}\ge \frac{{{\left( \left| z \right|+\left| {{z}_{1}} \right| \right)}^{2}}}{2};\,\,\forall z,\,{{z}_{1}}\). (2)

Áp dụng (1) và (2), ta có:

\({{\left| z-3-2i+3 \right|}^{2}}+{{\left| z-3-2i-3 \right|}^{2}}=2\left( {{\left| z-3-2i \right|}^{2}}+9 \right)\).

\({{\left| z-3-2i+3 \right|}^{2}}+{{\left| z-3-2i-3 \right|}^{2}}\ge \frac{{{\left( \left| z-3-2i+3 \right|+\left| z-3-2i-3 \right| \right)}^{2}}}{2}=\frac{{{\left( \left| z-2i \right|+\left| z-6-2i \right| \right)}^{2}}}{2}\).

Vậy, ta có: \(\frac{{{\left( \left| z-2i \right|+\left| z-6-2i \right| \right)}^{2}}}{2}\le 2\left( {{\left| z-3-2i \right|}^{2}}+9 \right)\Rightarrow {{\left( \left| z-2i \right|+\left| z-6-2i \right| \right)}^{2}}\le 4\left( {{\left| z-3-2i \right|}^{2}}+9 \right)\).

\(\Rightarrow {{P}^{2}}\le 4\left( {{\left| z-3-2i \right|}^{2}}+9 \right)\).

Do \(4\left( {{\left| z-3-2i \right|}^{2}}+9 \right)=4\left( {{\left| z-3+2i-4i \right|}^{2}}+9 \right)\) nên \({{P}^{2}}\le 4\left( {{\left( \left| z-3+2i \right|+\left| -4i \right| \right)}^{2}}+9 \right)\)

\(\Rightarrow {{P}^{2}}\le 4\left( {{7}^{2}}+9 \right)=232\Rightarrow P\le 2\sqrt{58}\).

Cách 2.

Ta có: \(5w=\left( 2+i \right)\left( z-4 \right)\) thay \(\left| \text{w}+i \right|=\frac{3\sqrt{5}}{5}\)

\(\Rightarrow \left| z-3+2i \right|=3\).

Suy ra, tập hợp các điểm biểu diễn số phức \(z\) là đường tròn \(\left( C \right):\,{{\left( x-3 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=9\).

Gọi \(M\in \left( C \right)\).

Ta có: \(P=\left| z-2i \right|+\left| z-6-2i \right|=AM+BM\,;\,\,A\left( 0\,;\,2 \right),\,B\left( 6\,;\,2 \right)\).

Suy ra \(P\le \sqrt{2\left( A{{M}^{2}}+B{{M}^{2}} \right)}\).

Gọi \(H\) là trung điểm của cạnh \(AB\).

Ta có: \(P\le \sqrt{2\left( A{{M}^{2}}+B{{M}^{2}} \right)}=\sqrt{2\left( 2M{{H}^{2}}+\frac{A{{B}^{2}}}{2} \right)}=\sqrt{4M{{H}^{2}}+A{{B}^{2}}}\).

Vậy, \(P=\left| z-2i \right|+\left| z-6-2i \right|\) đạt giá trị lớn nhất khi \(M{{H}^{2}}\) đạt giá trị lớn nhất.

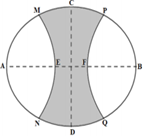
Dựa vào hình vẽ sau