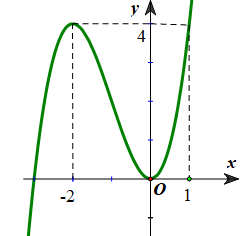
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ:
Tập hợp tất cả giá trị thực của tham số \(m\) để phương trình \(f\left( 2\sin x+1 \right)=m\) có nghiệm thuộc nửa khoảng \(\left[ 0\,;\frac{\pi }{6} \right)\) là?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn A
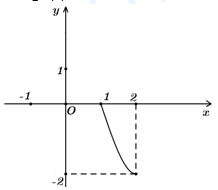
Đặt \(2\sin x+1=t\). Khi \(x\in \left[ 0\,;\frac{\pi }{6} \right)\) thì \(t\in \left[ 1\,;2 \right)\). Bài toán trở thành tìm điều kiện của \(m\) để phương trình \(f\left( t \right)=m\) có nghiệm trên nửa khoảng \(\left[ 1\,;2 \right)\). Từ đồ thị hàm số \(f\left( x \right)\) ta suy ra đồ thị của hàm số \(f\left( t \right)\) trên \(\left[ 1\,;2 \right)\) như sau:
Dựa vào đồ thị: Phương trình \(f\left( t \right)=m\) có nghiệm trên \(\left[ 1\,;2 \right)\) khi và chỉ khi \(-2<m \le 0\).
Vậy tập hợp tất cả giá trị thực của tham số \(m\) để phương trình \(f\left( 2\sin x+1 \right)=m\) có nghiệm thuộc nửa khoảng \(\left[ 0\,;\frac{\pi }{6} \right)\) là \(\left( -2\,;0 \right]\).
Chọn A
Đề thi thử Tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Trần Hữu Trang



.PNG)