Trắc nghiệm Mệnh đề Toán Lớp 10
-
Câu 1:
Trong các câu sau, có bao nhiêu câu là không phải là mệnh đề? a) Hà Nội là một thành phố của Việt Nam. b) Sông Hồng chảy ngang qua thành phố Huế. c) Hãy trả lời câu hỏi này! d) 5 + 19 = 24. e) 6 + 81 = 25. f) Bạn có rỗi tối nay không?
A. 5
B. 2
C. 3
D. 4
-
Câu 2:
Cho các phát biểu sau, số phát biểu là mệnh đề là: +) Trái đất hình elip. +) Các em hãy cố gắng học tập! +) Một tam giác cân thì mỗi góc đều bằng 600 phải không?
A. 0
B. 1
C. 2
D. 3
-
Câu 3:
Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. Nếu a≥b thì a2≥b2.
B. Nếu a chia hết cho 9 thì aa chia hết cho 3.
C. Nếu một tam giác có một góc bằng 900 thì tam giác đó vuông
D. Một tam giác vuông thì có một góc bằng 900
-
Câu 4:
Mệnh đề nào sau đây sai?
A. Hai tam giác có diện tích bằng nhau thì bằng nhau
B. Hai tam giác bằng nhau thì có diện tích bằng nhau
C. Tam giác có ba cạnh bằng nhau thì có ba góc bằng nhau
D. Tam giác có ba góc bằng nhau thì có ba cạnh bằng nhau
-
Câu 5:
Khẳng định nào sau đây sai?
A. “Mệnh đề” là từ gọi tắt của “mệnh đề logic”.
B. Mệnh đề là một câu khẳng định đúng hoặc một câu khẳng định sai.
C. Mệnh đề có thể vừa đúng hoặc vừa sai.
D. Một khẳng định đúng gọi là mệnh đề đúng, một khẳng định sai gọi là mệnh đề sai.
-
Câu 6:
Với tập hợp X có hữu hạn phần tử, kí hiệu |X| là số phần tử của X. Cho A, B là hai tập hợp hữu hạn phần tử, sắp xếp các số |A|, |A∪B|, |A∩B| theo thứ tự không giảm, ta được:
A. |A∩B|, |A∪B|, |A|
B. |A|, |A∩B|, |A∪B|
C. |A∩B|, |A|, |A∪B|
D. |A∪B|, |A|, |A∩B|
-
Câu 7:
Cho các tập hợp A, B. Miền tô đậm trong hình vẽ bênbiểu diễn tập hợp nào dưới đây?
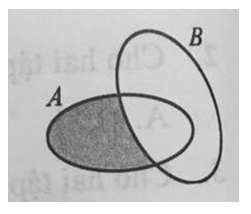
A. A∩B
B. B\A
C. CAB
D. CA(A∩B)
-
Câu 8:
Cho hai tập hợp A, B thỏa mãn A ⊂ B . Trong các mệnh đề sau, mệnh đề nào sai?
A. A∩B = A
B. A∪B = B
C. A\B = ∅
D. B\A = B
-
Câu 9:
Cho tập hợp X và các mệnh đề:
(I) X∪X = X
(II) X∩X = X
(III) X∪∅ = ∅
(IV) ∅∪X = ∅
(V) X\X = X
(VI) ∅\X = ∅
(VII) X\∅ = ∅
Trong các mệnh đề trên, có bao nhiêu mệnh đề là đúng?
A. 3
B. 4
C. 5
D. 6
-
Câu 10:
Cho hai đa thức P(x) và Q(x). Xét các tập hợp sau:
A = {x∈R:P(x) = 0}; B = {x∈R:Q(x) = 0}; C = {x∈R:P(x).Q(x) = 0}
Trong các mệnh đề sau, mệnh đề nào đúng?
A. C = A\B
B. C = B\A
C. C = A∩B
D. C = A∪B
-
Câu 11:
Cho hai đa thức P(x) và Q(x). Xét các tập hợp sau:
A = {x∈R:P(x) = 0} ; B = {x∈R:Q(x) = 0}; C = {x∈R:[P(x)]2+[Q(x)]2 = 0}
Trong các mệnh đề sau, mệnh đề nào đúng?
A. C = A∪B
B. C = A∩B
C. C = A\B
D. C = B\A
-
Câu 12:
Cho hai đa thức P(x) và Q(x). Xét các tập hợp sau:
A = {x∈R:P(x) = 0}; B = {x∈R:Q(x) = 0}; C = {x∈R:P(x)/Q(x) = 0}
Trong các mệnh đề sau, mệnh đề nào đúng?
A. C = A∩B
B. C = A∪B
C. C = A\B
D. C = B\A
-
Câu 13:
Hãy chọn khẳng định đúng trong các khẳng định sau
A. \(x \in A\backslash B \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x \in A}\\ {x \notin B} \end{array}} \right.\)
B. \(x \in A\backslash B \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {x \in A}\\ {x \in B} \end{array}} \right.\)
C. \(x \in A\backslash B \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {x \in B}\\ {x \notin A} \end{array}} \right.\)
D. \(x \in A\backslash B \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {x \in A}\\ {x \notin B} \end{array}} \right.\)
-
Câu 14:
Cho các tập hợp A = {1;2;3;4;5}, B = {3;4;5;6;7}. Tập hợp (A\B)∪(B\A) bằng:
A. {1;2}
B. {6;7}
C. ∅
D. {1;2;6;7}
-
Câu 15:
Cho hai tập hợp A = {2;4;5;8} và B = {1;2;3;4}. Tập hợp A\B bằng tập hợp nào sau đây?
A. ∅
B. {2;4}
C. {5;8}
D. {5;8;1;3}
-
Câu 16:
Cho hai tập hợp M = {1;3;6;8} và N = {3;6;7;9}. Tập hợp M∪N là:
A. {1;8}
B. {7;9}
C. {1;7;8;9}
D. {1;3;6;7;8;9}
-
Câu 17:
Cho A = {a,b,c,d,e} và B = {c,d,e,k}. Tập hợp A ∩ B là:
A. {a,b}
B. {c,d,e}
C. {a,b,c,d,e,k}
D. {a,b,k}
-
Câu 18:
Gọi T là tập hợp các học sinh của lớp 10A; N là tập hợp các học sinh nam và G là tập hợp các học sinh nữ của lớp 10A. Xét các mệnh đề sau:
(I) N∪G = T
(II) N∪T = G
(III) N∩G = ∅
(IV) T∩G = N
(V) T\N = G
(VI) N\G = N
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?
A. 2
B. 3
C. 4
D. 5
-
Câu 19:
Tìm x, y để ba tập hợp A = {2;5}, B = {5;x}, C = {x;y;5} bằng nhau
A. x = y = 2
B. x = y = 2 hoặc x = 2, y = 5
C. x = 2, y = 5
D. x = 5, y = 2 hoặc x = y = 5
-
Câu 20:
Cho tập hợp \(A = \left\{ {x \in R/{x^2} + 3x + 4 = 0} \right\}\), kết luận nào sau đây là đúng?
A. Tập hợp A có 1 phần tử
B. Tập hợp A có 2 phần tử
C. Tập hợp A = ∅
D. Tập hợp A có vô số phần tử
-
Câu 21:
Cho tập A gồm các số tự nhiên có 1 chữ số. Số các tập con của A gồm hai phần tử, trong đó có phần tử 0 là:
A. 32
B. 324
C. 36
D. 9
-
Câu 22:
Tập A = {0;2;4;6} có bao nhiêu tập hợp con có đúng hai phần tử?
A. 4
B. 6
C. 7
D. 8
-
Câu 23:
Cho tập A = {1;2;3;4;5;6}. Số các tập con khác nhau của A gồm hai phần tử là:
A. 13
B. 15
C. 11
D. 17
-
Câu 24:
Cho tập X = {1;2;3;4}. Khẳng định nào sau đây đúng?
A. Số tập con của X là 16
B. Số tập con của X có hai phần tử là 8
C. Số tập con của X chứa số 1 là 6
D. Số tập con của X chứa 4 phần tử là 0
-
Câu 25:
Cho tập X = {2;3;4}. Hỏi tập X có bao nhiêu tập hợp con?
A. 3
B. 6
C. 8
D. 9
-
Câu 26:
Cho A = {1,2,3). Hãy chọn câu trả lời đúng trong các câu sau:
A. A có 3 tập hợp con
B. A có 5 tập hợp con
C. A có 6 tập hợp con
D. A có 8 tập hợp con
-
Câu 27:
Số phần tử của tập \(A = \left\{ {{{\left( { - 1} \right)}^2}^{n + 1},n \in N*} \right\}A = \left\{ {{{\left( { - 1} \right)}^2}^{n + 1},n \in N*} \right\}\) là:
A. 3
B. 1
C. Vô số
D. 2
-
Câu 28:
Cách viết nào sau đây là đúng?
A. {a} ∈ [a;b]
B. {a} ∈ [a;b]
C. a ∈ (a;b]
D. {a} ⊂ [a;b]
-
Câu 29:
Mệnh đề nào sau đây là mệnh đề sai?
A. {a} ∈ {a;b}
B. {a} ⊂ {a}
C. a ∈ {a}
D. ∅ ⊂ {a}
-
Câu 30:
Hãy liệt kê các phần tử của tập X = {x∈R| x2+x+1 = 0}
A. X = 0
B. X = {0}
C. X = ∅
D. X = {∅}
-
Câu 31:
Cho tập hợp \(A = \left\{ {x \in R\left| {{x^4} - 6{x^2} + 8 = 0} \right.} \right\}.\) Số phần tử của tập A là:
A. 1
B. 2
C. 3
D. 4
-
Câu 32:
Hãy liệt kê các phần tử của tập X = {x∈R|2x2−5x+3 = 0}
A. X = {0}
B. X = {1}
C. \(X = \left\{ {\frac{3}{2}} \right\}\)
D. \(X = \left\{ {1;\frac{3}{2}} \right\}\)
-
Câu 33:
Cho tập hợp \(A = \left\{ {x \in \left. R \right|\left( {{x^2} - 1} \right)\left( {{x^2} + 2} \right) = 0} \right\}.\). Tập hợp A là:
A. A = {-1; 1}
B. \(A = \left\{ { - \sqrt 2 ; - 1;1;\sqrt 2 } \right\}\)
C. A = {-1}
D. A = {1}
-
Câu 34:
Mệnh đề nào sau đây tương đương với mệnh đề A ≠ ∅ ?
A. ∀x,x ∈ A
B. ∃x, x ∈ A
C. ∃x, x ∉ A
D. ∀x, x ⊂ A
-
Câu 35:
Trong các mệnh đề sau, tìm mệnh đề nào sai?
A. A ∈ A
B. ∅ ⊂ A
C. A ⊂ A
D. A ≠ {A}
-
Câu 36:
Cho x là một phần tử của tập hợp A. Xét các mệnh đề sau:
x ∈ A
{x} ∈ A
x ⊂ A
{x} ⊂ ATrong các mệnh đề trên, mệnh đề nào đúng?
A. I và II
B. I và III
C. I và IV
D. II và IV
-
Câu 37:
Cho A = {1;2;3}. Trong các khẳng định sau, khẳng định nào sai?
A. ∅ ⊂ A
B. 1 ∈ A
C. {1;2} ⊂ A
D. 2 = A
-
Câu 38:
Kí hiệu nào sau đây dùng để viết đúng mệnh đề “ \(\sqrt 2 \) không phải là số hữu tỉ”?
A. \(\sqrt 2 \ne Q\)
B. \(\sqrt 2 \not\subset Q\)
C. \(\sqrt 2 \notin Q\)
D. \(\sqrt 2 \in Q\)
-
Câu 39:
Cho mệnh đề: “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau”. Mệnh đề nào sau đây tương đương với mệnh đề đã cho?
A. Điều kiện cần để tứ giác là hình thang cân là tứ giác đó có hai đường chéo bằng nhau
B. Điều kiện đủ để tứ giác có hai đường chéo bằng nhau là tứ giác đó là hình thang cân
C. Điều kiện đủ dể tứ giác là hình thang cân là tứ giác đó có hai đường chéo bằng nhau
D. Cả A, B đều đúng
-
Câu 40:
Các phát biểu nào sau đây không thể là phát biểu của mệnh đề đúng P ⇒ Q
A. Nếu P thì Q
B. P kéo theo Q
C. P là điều kiện đủ để có Q
D. P là điều kiện cần để có Q
-
Câu 41:
Cho hai mệnh đề P và Q. Tìm điều kiện để mệnh đề P⇔Q đúng
A. P đúng và Q sai
B. P đúng và Q đúng
C. P sai và Q đúng
D. P và Q cùng đúng hoặc cùng sai
-
Câu 42:
Cho hai mệnh đề P và Q. Phát biểu nào sau đây sai về mệnh đề đúng P ⇔ Q?
A. P khi và chỉ khi Q
B. P tương đương Q
C. P là điều kiện cần để có Q
D. P là điều kiện cần và đủ để có Q
-
Câu 43:
Trong các mệnh đề sau, mệnh đề nào không phải là định lí?
A. Điều kiện đủ để trong mặt phẳng, hai đường thẳng song song với nhau là hai đường thẳng ấy cùng vuông góc với đường thẳng thứ ba.
B. Điều kiện đủ để diện tích ta giác bằng nhau là hai ta giác ấy bằng nhau.
C. Điều kiện đủ để hai đường chéo của một tứ giác vuông góc với nhau là tứ giác ấy là hình thoi.
D. Điều kiện đủ để một số nguyên dương a có tận cùng bằng 5 là số đó chia hết cho 5.
-
Câu 44:
Phủ định của mệnh đề P(x): "∃x∈R,5x−3x2 = 1" là:
A. "∃x∈R,5x−3x2 = 1"
B. "∀x∈R,5x−3x2 = 1"
C. "∀x∈R,5x−3x2 ≠ 1"
D. "∃x∈R,5x−3x2 ≥ 1"
-
Câu 45:
Mệnh đề phủ định của mệnh đề P(x):"∃x∈R : x2+2x+5 là số nguyên tố” là:
A. \(\forall x \notin R:{x^2} + 2x + 5\) là hợp số
B. \(\exists x \in R:{x^2} + 2x + 5\) là hợp số
C. \(\forall x \in R:{x^2} + 2x + 5\) là hợp số
D. \(\exists x \in R:{x^2} + 2x + 5\) là số thực
-
Câu 46:
Mệnh đề phủ định của mệnh đề P(x): “x2 + 3x + 1 > 0 với mọi x” là:
A. Tồn tại x sao cho x2 + 3x + 1 > 0
B. Tồn tại x sao cho x2 + 3x + 1 ≤ 0
C. Tồn tại x sao cho x2 + 3x + 1 = 0
D. Tồn tại x sao cho x2 + 3x + 1 < 0
-
Câu 47:
Cho mệnh đề “∀x∈R, x2 < x”. Trong các mệnh đề sau, mệnh đề nào là phủ định của mệnh đề?
A. \(\exists x \in R,{x^2} < x\)
B. \(\exists x \in R,{x^2} \ge x\)
C. \(\forall x \in R,{x^2} < x\)
D. \(\forall x \in R,{x^2} \ge x\)
-
Câu 48:
Mệnh đề \(P\left( x \right):\forall x \in R,{x^2} - x + 7 < 0\). Phủ định của mệnh đề P là:
A. \(\exists x \in R,{x^2} - x + 7 > 0\)
B. \(\forall x \in R,{x^2} - x + 7 > 0\)
C. \(\forall x \notin R,{x^2} - x + 7 \ge 0\)
D. \(\exists x \in R,{x^2} - x + 7 \ge 0\)
-
Câu 49:
Tìm mệnh đề phủ định của mệnh đề P:"∀x∈R, 2x−9 = 0"
A. \(\bar P:\forall x \in R,2x - 9 < 0\)
B. \(\bar P:\forall x \in R,2x - 9 \ne 0\)
C. \(\bar P:\exists x \in R,2x - 9 \ge 0\)
D. \(\bar P:\exists x \in R,2x - 9 \ne 0\)
-
Câu 50:
Cho x là số thực, mệnh đề nào sau đây đúng?
A. \(\forall x,{x^2} > 5 \Rightarrow x > \sqrt 5 \) hoặc \(x < - \sqrt 5 \)
B. \(\forall x,{x^2} > 5 \Rightarrow - \sqrt 5 < x < \sqrt 5 \)
C. \(\forall x,{x^2} > 5 \Rightarrow x > \pm \sqrt 5 \)
D. \(\forall x,{x^2} > 5 \Rightarrow x \ge \sqrt 5 \) hoặc \(x \le -\sqrt 5 \)
