ADMICRO
Tính tích phân ta được kết quả:
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ZUNIA12
Lời giải:
Báo saiCho 1 = 0 ⇔ x = (thỏa mãn)
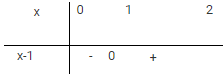
Ta có bảng xét dấu:
Khi đó
ZUNIA9
AANETWORK