ADMICRO
Số các giá trị nguyên của tham số m để phương trình log√2(x−1)=log2(mx−8)log√2(x−1)=log2(mx−8) có hai nghiệm thực phân biệt là:
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Môn: Toán Lớp 12
ZUNIA12
Lời giải:
Báo sailog√2(x−1)=log2(mx−8)⇔{x−1>0mx−8>0(x−1)2=mx−8⇔{x>1(x−1)2=mx−8⇔{x>1m=x2−2x+9xlog√2(x−1)=log2(mx−8)⇔⎧⎪⎨⎪⎩x−1>0mx−8>0(x−1)2=mx−8⇔{x>1(x−1)2=mx−8⇔{x>1m=x2−2x+9x
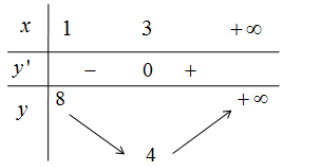
Xét hàm số y=x2−2x+9x trên (1;+∞) , ta có y′=x2−9x2 . Giải y′=0⇔x=±3 Bảng biến thiên
Để thỏa mãn yêu cầu thì 4<m<8 nên các giá trị nguyên của tham số m là 5,6,7 .
ZUNIA9
AANETWORK