Gọi \({z_1}, {z_2}\) là hai trong các số phức thỏa mãn \(\left| {z – 1 + 2i} \right| = 5\) và \(\left| {{z_1} – {z_2}} \right| = 8\). Tìm môđun của số phức \(w = {z_1} + {z_2} – 2 + 4i\).
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai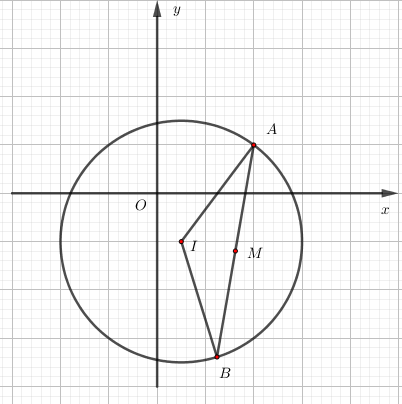
Gọi A là điểm biểu diễn của số phức \({z_1}\), B là điểm biểu diễn của số phức \({z_2}\).
Theo giả thiết \({z_1}, {z_2}\) là hai trong các số phức thỏa mãn \(\left| {z – 1 + 2i} \right| = 5\) nên A và B thuộc đường tròn tâm \(I\left( {1; – 2} \right)\) bán kính r = 5.
Mặt khác \(\left| {{z_1} – {z_2}} \right| = 8 \Leftrightarrow AB = 8\).
Gọi M là trung điểm của AB suy ra M là điểm biểu diễn của số phức \(\frac{{{z_1} + {z_2}}}{2}\) và IM = 3.
Do đó ta có
\(3 = IM = \left| {\frac{{{z_1} + {z_2}}}{2} – 1 + 2i} \right| \Leftrightarrow 3 = \frac{1}{2}\left| {{z_1} + {z_2} – 2 + 4i} \right| \Leftrightarrow \left| {{z_1} + {z_2} – 2 + 4i} \right| = 6 \Leftrightarrow \left| w \right| = 6\)
