ADMICRO
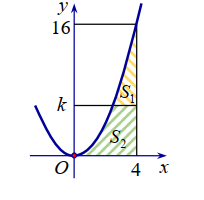
Cho hàm số y=f(x) xác định và liên tục trên biết và với . Tính ?
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ZUNIA12
Lời giải:
Báo sai
ZUNIA9
AANETWORK