Gọi \(S\) là tập hợp tất cả các giá trị nguyên của \(m\) thuộc đoạn \(\left[ -2022;2022 \right]\) để hàm số \(y=\ln \left( {{x}^{2}}+1 \right)-mx\) đồng biến trên khoảng \(\left( 0;+\infty \right)\). Số phần tử của \(S\) là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn C
Ta có \({y}'=\frac{2x}{{{x}^{2}}+1}-m\)
Hàm số \(y=\ln \left( {{x}^{2}}+1 \right)-mx\) đồng biến trên khoảng \(\left( 0;+\infty \right)\):
\(\Leftrightarrow {y}'=\frac{2x}{{{x}^{2}}+1}-m\ge 0,\forall x\in \left( 0;+\infty \right)\)\(\Leftrightarrow m\le \frac{2x}{{{x}^{2}}+1},\forall x\in \left( 0;+\infty \right)\)
Xét hàm số \(f\left( x \right)=\frac{2x}{{{x}^{2}}+1}\), ta có \({f}'\left( x \right)=\frac{2\left( {{x}^{2}}+1 \right)-2x.2x}{{{\left( {{x}^{2}}+1 \right)}^{2}}}=\frac{-2{{x}^{2}}+2}{{{\left( {{x}^{2}}+1 \right)}^{2}}}=0\)
\(\Leftrightarrow \left[ \begin{matrix} x=1 & \left( n \right) \\ x=-1 & \left( l \right) \\ \end{matrix} \right.\)
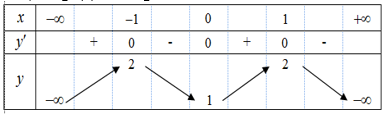
Bảng biến thiên:
.PNG)
Từ bảng biến thiên, \(m\le \frac{2x}{{{x}^{2}}+1},\forall x\in \left( 0;+\infty \right)\Leftrightarrow m\le 0\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Chuyên Trần Phú
Câu hỏi liên quan
-
Cắt mặt cầu \(\left( S \right)\) bằng một mặt phẳng cách tâm một khoảng bằng 4 \(\text{cm}\) ta được một thiết diện là đường tròn có bán kính bằng \(3\)\(\text{cm}\). Bán kính của mặt cầu \(\left( S \right)\) là
-
Có bao nhiêu số nguyên \(x\in \left[ -2022;2022 \right]\) thỏa mãn \(\left( {{3}^{{{x}^{2}}}}-{{27}^{x}} \right)\sqrt{{{\log }_{2}}\left( 4x \right)-2}\ge 0\)?
-
Khối chóp có diện tích đáy là \(B\), chiều cao bằng \(h\). Thể tích \(V\) của khối chóp là
-
Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A\), biết \(AB=a,\,\,AC=2a\). Mặt bên \(\left( SAB \right)\) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo \(a\) thể tích khối chóp \(S.ABC\).
-
Tìm tung độ giao điểm của đồ thị \(\left( C \right):y=\frac{2x-3}{x+3}\) và đường thẳng \(d:y=x-1\).
-
Cho hàm số \(y=f\left( x \right)\)có bảng biến thiên như sau
.PNG)
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
-
Có bao nhiêu cặp số nguyên \((x, y)\) thỏa mãn \(x+y>0,-20 \leq x \leq 20\) và \(\log _2(x+2 y)+x^2+2 y^2+3 x y-x-y=0\)
-
Tập nghiệm của phương trình \({{2}^{x}}=-1\) là
-
Hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\)và có bảng biến thiên như sau:
Biết \(f\left( -4 \right)>f\left( 8 \right)\), khi đó giá trị nhỏ nhất của hàm số đã cho trên \(\mathbb{R}\)bằng
-
Cho hàm số bậc bốn \(y=f(x)\)có đồ thị hàm số \(y={f}'\left( x \right)\) như hình vẽ bên. Hàm số \(g\left( x \right)=4f\left( {{x}^{2}}-4 \right)+{{x}^{4}}-8{{x}^{2}}\) có bao nhiêu điểm cực tiểu?
-
Có bao nhiêu giao điểm của đồ thị hàm số \(y={{x}^{3}}+3x-3\) với trục \(Ox\)?
-
Với các số thực dương \(a\), \(b\) bất kì, mệnh đề nào dưới đây sai?
-
Thể tích của khối hình hộp chữ nhật có các kích thước lần lượt là \(a\);\(2a\);\(3a\) bằng bao nhiêu?
-
Cho hàm số \(y=f(x)\) liên tục trên \(R\) và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\)để phương trình \(f\left( f(\cos x) \right)=m\) có nghiệm thuộc khoảng \(\left( \frac{\pi }{2};\frac{3\pi }{2} \right)?\)
.PNG)
A. \(5.\) B. \(3.\) C. \(4.\) D. \(2.\)
-
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
.PNG)
Phương trình \(f\left( x \right)=4\) có bao nhiêu nghiệm thực?
-
Cho hình nón có chiều cao bằng \(8\,\text{cm}\), bán kính đáy bằng \(6\,\text{cm}\). Diện tích toàn phần của hình nón đã cho bằng
-
Cho hàm số \(f\left( x \right)={{x}^{3}}-3{{x}^{2}}+mx-2\) đạt cực tiểu tại \(x=2\) khi
-
Cho hàm số \(y=f(x)\) xác định trên \(\mathbb{R}\)và có bảng xét dấu:
Hàm số \(f(x)\) có bao nhiêu điểm cực trị?
-
Tổng tất cả các nghiệm của phương trình \({{3}^{2x}}-{{4.3}^{x}}+3=0\) bằng
-
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
Hàm số \(y=f\left( x \right)\)đồng biến trên khoảng nào dưới đây?
