Cho phương trình \({3^x} + m = {\log _3}\left( {x - m} \right)\) với m là tham số. Có bao nhiêu giá trị nguyên của \(m \in \left( { - 15;15} \right)\) để phương trình đã cho có nghiệm ?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \({\log _3}\left( {x - m} \right) = y \Leftrightarrow x - m = {3^y} \Leftrightarrow x = m + {3^y}\)
Ta có hệ : \(\left\{ \begin{array}{l}{3^x} + m = y\,\,\,\left( 1 \right)\\{3^y} + m = x\,\,\,\left( 2 \right)\end{array} \right.\)
Trừ vế cho vế của \(\left( 1 \right)\) cho \(\left( 2 \right)\) ta được \({3^x} + x = {3^y} + y\,\,\,\left( * \right)\)
Xét \(f\left( t \right) = {3^t} + t \Rightarrow f'\left( t \right) = {3^t}\ln 3 + 1 > 0,\forall t\) suy ra hàm số đồng biến trên \(R\)
\(\left( * \right) \Leftrightarrow x = y\). Khi đó \(\left( 1 \right) \Leftrightarrow m = x - {3^x}\)
Xét \(g\left( x \right) = x - {3^x} \Rightarrow g'\left( x \right) = 1 - {3^x}\ln 3 = 0 \Leftrightarrow x = {\log _3}\frac{1}{{\ln 3}}\)
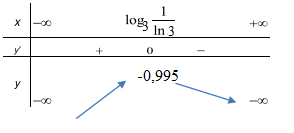
Do đó \(m < - 0,995\), mà \(m \in \left( { - 15;15} \right)\) nên \(m \in \left\{ { - 14; - 13;...; - 1} \right\}\)
Vậy có \(14\) giá trị nguyên của \(m\)
Chọn C.
Đề thi thử THPT QG năm 2023 môn Toán
Trường THPT Trần Hưng Đạo
Câu hỏi liên quan
-
Trong không gian Oxyz, mặt phẳng \(\left( P \right):\,3x + 2y + z - 4 = 0\) có một vecto pháp tuyến là
-
Số phức có phần thực bằng 3 và phần ảo bằng 4 là:
-
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx - 2\) và \(g\left( x \right) = d{x^2} + ex + 2\,\,\left( {a,b,c,d,e \in R} \right).\) Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 2; - 1;1\) (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng:
-
Cho hàm số \(y = \frac{{x - 1}}{{x + 1}}\) có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của (C). Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn thẳng AB có độ dài bằng
-
Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B, \(AB = a,SA\) vuông góc với mặt phẳng đáy và \(SA = a.\) Khoảng cách từ A đến mặt phẳng (SBC) bằng
-
Cho khối chóp có đáy là hình vuông cạnh a và chiều cao bằng 4a. Thể tích của khối chóp đã cho bằng
-
Cho \(\int\limits_5^{21} {\frac{{dx}}{{x\sqrt {x + 4} }} = a\ln 3} + b\ln 5 + c\ln 7\) với \(a,\,b,\,c\) là các số hữu tỉ. Mệnh đề nào dưới đây đúng?
-
Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là \(a\sqrt 3 .\) Thể tích V của khối chóp đó là bao nhiêu?
-
Cho \(a > 0,b > 0\) thỏa mãn \({\log _{10a + 3b + 1}}\left( {25{a^2} + {b^2} + 1} \right) + {\log _{10ab + 1}}\left( {10a + 3b + 1} \right) = 2\) . Giá trị của \(a + 2b\) bằng:
-
Cho hình chóp S.ABCD có đáy là hình chữ nhật, \(AB = a,BC = 2a,\,SA\) vuông góc với mặt phẳng đáy và \(SA = a.\) Khoảng cách giữa hai đường thẳng BD và SC bằng
-
Trong không gian Oxyz, cho đường thẳng d : \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - 3\\z = 5 + 4t\end{array} \right..\) Gọi \(\Delta \) là đường thẳng đi qua điểm \(A\left( {1; - 3;5} \right)\) và có vecto chỉ phương \(\overrightarrow u \left( {1;2; - 2} \right).\) Đường phân giác của góc nhọn tạo bởi d và \(\Delta \) có phương trình là
-
Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v\left( t \right) = \frac{1}{{150}}{t^2} + \frac{{59}}{{75}}t\,\,\left( {m/s} \right)\) , trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 3 giây so với A và có gia tốc bằng \(a\left( {m/{s^2}} \right)\) (a là hằng số). Sau khi B xuất phát được 12 giây thì đuổi kịp A. Vận tốc của B tại thời điểm đuổi kịp A bằng
-
Cho hai hàm số \(y = f\left( x \right)\) và \(y=g\left( x \right).\) Hai hàm số \(y=f'\left( x \right)\) và \(y = g'\left( x \right)\) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số \(y = g'\left( x \right)\). Hàm số \(h\left( x \right) = f\left( {x + 7} \right) - g\left( {2x + \frac{9}{2}} \right)\) đồng biến trên khoảng nào dưới đây ?
-
Trong không gian Oxyz, mặt phẳng đi qua điểm \(A\left( {1;2; - 2} \right)\) và vuông góc với đường thẳng \(\Delta :\frac{{x + 1}}{2} = \frac{{y - 2}}{1} = \frac{{z + 3}}{3}\) có phương trình là
-
Cho hình lập phương ABCD. A’B’C’D’ có tâm O. Gọi I là tâm của hình vuông A’B’C’D’ và M là điểm thuộc đoạn thẳng OI sao cho \(MO = \frac{1}{2}MI\) (tham khảo hình vẽ). Khi đó cosin của góc tạo bởi hai mặt phẳng (MC’D’) và (MAB) bằng
-
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^2} + c\left( {a,b,c \in R} \right).\) Đồ thị của hàm số \(y = f\left( x \right)\) như hình vẽ bên. Số nghiệm thực của phương trình \(4f\left( x \right) - 3 = 0\) là:
-
Từ một hộp chứa 7 quả cầu màu đỏ và 5 quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác suất để lấy được 3 quả cầu màu xanh bằng
-
Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm 38 học sinh?
-
Cho hàm số \(y = \frac{1}{8}{x^4} - \frac{7}{4}{x^2}\) có đồ thị (C). Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt \(M\left( {{x}_{1}};{{y}_{1}} \right),N\left( {{x}_{2}};{{y}_{2}} \right)\) ( M, N khác A) thỏa mãn \({y_1} - {y_2} = 3\left( {{x_1} - {x_2}} \right)?\)
-
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
