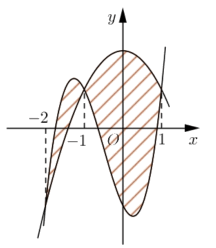
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx - 2\) và \(g\left( x \right) = d{x^2} + ex + 2\,\,\left( {a,b,c,d,e \in R} \right).\) Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 2; - 1;1\) (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có:
\(a{x^3} + b{x^2} + cx - 2 = d{x^2} + ex + 2 \Leftrightarrow a{x^3} + \left( {b - d} \right){x^2} + \left( {c - e} \right)x - 4 = 0\,\,\left( 1 \right)\)
Vì phương trình \(\left( 1 \right)\) có các nghiệm \( - 2; - 1;1\) nên:
\(\left\{ \begin{array}{l}a{\left( { - 2} \right)^3} + \left( {b - d} \right){\left( { - 2} \right)^2} + \left( {c - e} \right)\left( { - 2} \right) - 4 = 0\\a{\left( { - 1} \right)^3} + \left( {b - d} \right){\left( { - 1} \right)^2} + \left( {c - e} \right)\left( { - 1} \right) - 4 = 0\\a{.1^3} + \left( {b - d} \right){.1^2} + \left( {c - e} \right).1 - 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b - d = 4\\c - e = - 2\end{array} \right.\)
Diện tích hình phẳng cần tìm là:
\(\begin{array}{l}S = \int\limits_{ - 2}^{ - 1} {\left( {f\left( x \right) - g\left( x \right)} \right)dx + } \int\limits_{ - 1}^1 {\left( {g\left( x \right) - f\left( x \right)} \right)dx} \\ = \int\limits_{ - 2}^{ - 1} {\left( {a{x^3} + \left( {b - d} \right){x^2} + \left( {c - e} \right)x - 4} \right)dx + } \int\limits_{ - 1}^1 {\left( { - a{x^3} + \left( {d - b} \right){x^2} + \left( {e - c} \right)x + 4} \right)dx} \\ = \int\limits_{ - 2}^{ - 1} {\left( {2{x^3} + 4{x^2} - 2x - 4} \right)dx + } \int\limits_{ - 1}^1 {\left( { - 2{x^3} - 4{x^2} + 2x + 4} \right)dx} \\ = \frac{5}{6} + \frac{{16}}{3} = \frac{{37}}{6}.\end{array}\)
Chọn A.
Đề thi thử THPT QG năm 2023 môn Toán
Trường THPT Trần Hưng Đạo
Câu hỏi liên quan
-
Gọi S là diện tích của hình phẳng giới hạn bởi các đường \(y = {2^x},y = 0,x = 0,x = 2.\) Mệnh đề nào dưới đây đúng?
-
Cho \(a > 0,b > 0\) thỏa mãn \({\log _{10a + 3b + 1}}\left( {25{a^2} + {b^2} + 1} \right) + {\log _{10ab + 1}}\left( {10a + 3b + 1} \right) = 2\) . Giá trị của \(a + 2b\) bằng:
-
Cho hai hàm số \(y = f\left( x \right)\) và \(y=g\left( x \right).\) Hai hàm số \(y=f'\left( x \right)\) và \(y = g'\left( x \right)\) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số \(y = g'\left( x \right)\). Hàm số \(h\left( x \right) = f\left( {x + 7} \right) - g\left( {2x + \frac{9}{2}} \right)\) đồng biến trên khoảng nào dưới đây ?
-
Có bao nhiêu số phức z thỏa mãn \(\left| z \right|\left( {z - 3 - i} \right) + 2i = \left( {4 - i} \right)z?\)
-
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a,b,c,d \in R} \right)\) có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là:
-
Cho hình lập phương ABCD. A’B’C’D’ có tâm O. Gọi I là tâm của hình vuông A’B’C’D’ và M là điểm thuộc đoạn thẳng OI sao cho \(MO = \frac{1}{2}MI\) (tham khảo hình vẽ). Khi đó cosin của góc tạo bởi hai mặt phẳng (MC’D’) và (MAB) bằng
-
Ba bạn A, B, C mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn \(\left[ {1;19} \right]\) . Xác suất để ba số được viết ra có tổng chia hết cho 3 bằng
-
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \frac{{x + 6}}{{x + 5m}}\) nghịch biến trên khoảng \(\left( {10; + \infty } \right)\) ?
-
Hệ số của \({x^5}\) trong khai triển biểu thức \(x{\left( {3x - 1} \right)^6} + {\left( {2x - 1} \right)^8}\) bằng
-
Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B, \(AB = a,SA\) vuông góc với mặt phẳng đáy và \(SA = a.\) Khoảng cách từ A đến mặt phẳng (SBC) bằng
-
Nguyên hàm của hàm số \(f\left( x \right) = {x^4} + x\) là
-
Giá trị nhỏ nhất của hàm số \(y = {x^3} + 2{x^2} - 7x\) trên đoạn \(\left[ {0;4} \right]\) bằng:
-
Xét các số phức z thỏa mãn \(\left( {\overline z + 3i} \right)\left( {z - 3} \right)\) là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng:
-
Trong không gian Oxyz, đường thẳng d: \(\frac{{x + 3}}{1} = \frac{{y - 1}}{{ - 1}} = \frac{{z - 5}}{2}\) có một vecto chỉ phương là
-
Cho hình chóp S.ABCD có đáy là hình chữ nhật, \(AB = a,BC = 2a,\,SA\) vuông góc với mặt phẳng đáy và \(SA = a.\) Khoảng cách giữa hai đường thẳng BD và SC bằng
-
Cho hàm số \(y = \frac{{x - 1}}{{x + 1}}\) có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của (C). Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn thẳng AB có độ dài bằng
-
Tập nghiệm của phương trình \({\log _2}\left( {{x^2} - 1} \right) = 3\) là:
-
Ông A dự định sử dụng hết \(6,7{m^2}\) kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
-
Cho phương trình \({3^x} + m = {\log _3}\left( {x - m} \right)\) với m là tham số. Có bao nhiêu giá trị nguyên của \(m \in \left( { - 15;15} \right)\) để phương trình đã cho có nghiệm ?
-
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
