Cho khối lăng trụ ABC.A’B’C’, khoảng cách từ C đến đường thẳng BB’ bằng \(\sqrt 5 \) , khoảng cách từ A đến các đường thẳng BB’ và CC’ lần lượt bằng 1 và 2, hình chiếu vuông góc của A lên mặt phẳng (A’B’C’) là trung điểm M của B’C’ và \(A'M = \frac{{\sqrt {15} }}{3}\) . Thể tích của khối lăng trụ đã cho bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai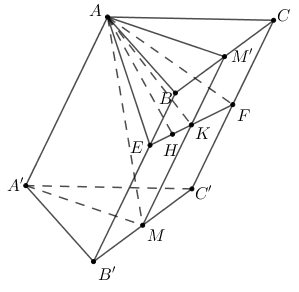
Gọi \(E,F\) lần lượt là hình chiếu vuông góc của A trên BB’,CC’ \( \Rightarrow AE = 1,AF = 2\)
Ta có: \(\begin{array}{l}\left\{ \begin{array}{l}BB' \bot AE\\BB' \bot AF\end{array} \right. \Rightarrow BB' \bot \left( {AEF} \right) \Rightarrow BB' \bot EF\\ \Rightarrow EF = d\left( {C,BB'} \right) = \sqrt 5 \end{array}\)
Ta có: \(A{E^2} + A{F^2} = {1^2} + {2^2} = 5 = E{F^2}\) Suy ra \(\Delta AEF\) vuông tại \(A\) .
Gọi M’ là trung điểm của BC
Gọi \(K = MM' \cap EF \Rightarrow K\) là trung điểm của \(EF\Rightarrow AK=\frac{1}{2}EF=\frac{\sqrt{5}}{2}.\) (do tam giác AEF vuông tại A và AK là đường trung tuyến)
Lại có \(MM'//BB' \Rightarrow MM' \bot \left( {AEF} \right) \Rightarrow MM' \bot AK\) . Lại có tam giác AMM’ vuông tại A có AK là đường cao nên:
\( \Rightarrow \frac{1}{{A{K^2}}} = \frac{1}{{A{M^2}}} + \frac{1}{{AM{'^2}}} \Rightarrow \frac{4}{5} = \frac{1}{{A{M^2}}} + \frac{9}{{15}} \Rightarrow AM = \sqrt 5 \)
Gọi \(H\) là hình chiếu vuông góc của \(A\) trên \(FE\Rightarrow AH\bot \left( BCC'B' \right)\)
Ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{E^2}}} + \frac{1}{{A{F^2}}} = \frac{1}{{{1^2}}} + \frac{1}{{{2^2}}} = \frac{5}{4} \Rightarrow AH = \frac{{2\sqrt 5 }}{5}\)
\(\begin{align} & MM{{'}^{2}}=A{{M}^{2}}+AM{{'}^{2}}=5+\frac{15}{9}=\frac{20}{3}\Rightarrow MM'=\frac{2\sqrt{15}}{3}=BB' \\ & {{S}_{BB'C'C}}=d\left( C,BB'\right).BB'=\sqrt{5}.\frac{2\sqrt{15}}{3}=\frac{10\sqrt{3}}{3} \\ & \Rightarrow{{V}_{ABC.A'B'C'}}=\frac{3}{2}{{V}_{ABCC'B'}}=\frac{3}{2}.\frac{1}{3}AH.{{S}_{BB'C'C}}=\frac{3}{2}.\frac{1}{3}.\frac{2\sqrt{5}}{5}.\frac{10\sqrt{3}}{3}=\frac{2\sqrt{15}}{3} \\ \end{align}\)
Chọn D.
Đề thi thử THPT QG năm 2023 môn Toán
Trường THPT Trần Hưng Đạo
Câu hỏi liên quan
-
Cho \(a > 0,b > 0\) thỏa mãn \({\log _{10a + 3b + 1}}\left( {25{a^2} + {b^2} + 1} \right) + {\log _{10ab + 1}}\left( {10a + 3b + 1} \right) = 2\) . Giá trị của \(a + 2b\) bằng:
-
Giá trị nhỏ nhất của hàm số \(y = {x^3} + 2{x^2} - 7x\) trên đoạn \(\left[ {0;4} \right]\) bằng:
-
Trong không gian Oxyz, cho điểm \(A\left( {2;1;3} \right)\) và đường thẳng \(d:\,\frac{{x + 1}}{1} = \frac{{y - 1}}{{ - 2}} = \frac{{z - 2}}{2}.\) Đường thẳng đi qua A, vuông góc với d và cắt trục Oy có phương trình là
-
Trong không gian Oxyz, mặt phẳng \(\left( P \right):\,3x + 2y + z - 4 = 0\) có một vecto pháp tuyến là
-
Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B, \(AB = a,SA\) vuông góc với mặt phẳng đáy và \(SA = a.\) Khoảng cách từ A đến mặt phẳng (SBC) bằng
-
Cho hàm số \(y = \frac{1}{8}{x^4} - \frac{7}{4}{x^2}\) có đồ thị (C). Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt \(M\left( {{x}_{1}};{{y}_{1}} \right),N\left( {{x}_{2}};{{y}_{2}} \right)\) ( M, N khác A) thỏa mãn \({y_1} - {y_2} = 3\left( {{x_1} - {x_2}} \right)?\)
-
Trong không gian Oxyz, cho hai điểm \(A\left( {1;1; - 2} \right)\) và \(B\left( {2;2;1} \right)\) . Vecto \(\overrightarrow {AB} \) có tọa độ là:
-
Cho hình lập phương ABCD. A’B’C’D’ có tâm O. Gọi I là tâm của hình vuông A’B’C’D’ và M là điểm thuộc đoạn thẳng OI sao cho \(MO = \frac{1}{2}MI\) (tham khảo hình vẽ). Khi đó cosin của góc tạo bởi hai mặt phẳng (MC’D’) và (MAB) bằng
-
Một người gửi tiết kiệm vào một ngân hàng với lãi suất 7,2%/ năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó thu được (cả số tiền gửi ban đầu và lãi) gấp đôi số tiền gửi ban đầu, giả định trong khoảng thời gian này lãi suất không thay đổi và người đó không rút tiền ra?
-
Cho hình chóp S.ABCD có đáy là hình chữ nhật, \(AB = a,BC = 2a,\,SA\) vuông góc với mặt phẳng đáy và \(SA = a.\) Khoảng cách giữa hai đường thẳng BD và SC bằng
-
Cho phương trình \({3^x} + m = {\log _3}\left( {x - m} \right)\) với m là tham số. Có bao nhiêu giá trị nguyên của \(m \in \left( { - 15;15} \right)\) để phương trình đã cho có nghiệm ?
-
Có bao nhiêu số phức z thỏa mãn \(\left| z \right|\left( {z - 3 - i} \right) + 2i = \left( {4 - i} \right)z?\)
-
Trong không gian Oxyz, đường thẳng d: \(\frac{{x + 3}}{1} = \frac{{y - 1}}{{ - 1}} = \frac{{z - 5}}{2}\) có một vecto chỉ phương là
-
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
-
Trong không gian Oxyz, cho mặt cầu (S) có tâm \(I\left( { - 1;2;1} \right)\) và đi qua điểm\(A\left( {1;0; - 1} \right)\) . Xét các điểm B, C, D thuộc (S) sao cho AB, AC, AD đôi một vuông góc với nhau. Thể tích khối tứ diện ABCD có giá trị lớn nhất bằng
-
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \frac{{x + 6}}{{x + 5m}}\) nghịch biến trên khoảng \(\left( {10; + \infty } \right)\) ?
-
Số phức có phần thực bằng 3 và phần ảo bằng 4 là:
-
Cho khối chóp có đáy là hình vuông cạnh a và chiều cao bằng 4a. Thể tích của khối chóp đã cho bằng
-
Cho hàm số \(f\left( x \right)\) thỏa mãn \(f\left( 2 \right) = - \frac{1}{3}\) và \(f'\left( x \right) = x{\left[ {f\left( x \right)} \right]^2}\) với mọi \(x \in \mathbb{R}\). Giá trị của \(f\left( 1 \right)\) bằng:
-
Trong không gian Oxyz, mặt phẳng đi qua điểm \(A\left( {1;2; - 2} \right)\) và vuông góc với đường thẳng \(\Delta :\frac{{x + 1}}{2} = \frac{{y - 2}}{1} = \frac{{z + 3}}{3}\) có phương trình là
