Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B, \(AB = a,SA\) vuông góc với mặt phẳng đáy và \(SA = a.\) Khoảng cách từ A đến mặt phẳng (SBC) bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai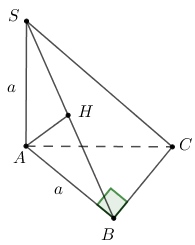
Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
BC \bot SA;{\mkern 1mu} BC \bot AB\\
\Rightarrow BC \bot \left( {SAB} \right);BC \subset \left( {SBC} \right)\\
\Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)
\end{array}\\
{\left( {SBC} \right) \cap \left( {SAB} \right) = SB}
\end{array}\)
Từ A kẻ AH vuông góc với (SBC) khi đó ta có: \(AH = d\left( {A;\left( {SBC} \right)} \right)\)
Áp dụng hệ thức lượng trong tam giác vuông SAB với AH là đường cao ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2}}} = \frac{2}{{{a^2}}} \Rightarrow AH = \frac{{a\sqrt 2 }}{2}\)
Chọn D.
Đề thi thử THPT QG năm 2023 môn Toán
Trường THPT Trần Hưng Đạo