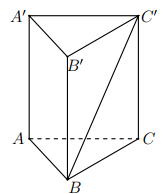
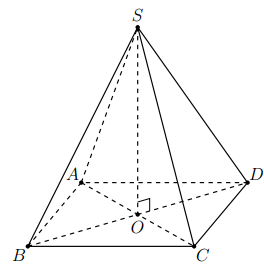
Cho lăng trụ tứ giác đều \(ABCD.A'B'C'D'\) có \(AC=4a.\) Gọi \(O\) là tâm của mặt \(A'B'C'D'.\) Biết rằng hai mặt phẳng \(\left( OAB \right)\) và \(\left( OCD \right)\) vuông góc với nhau. Thể tích khối lăng trụ \(ABCD.A'B'C'D'\) bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi \(O\) là tâm hình vuông suy ra \(SO\bot \left( ABCD \right)\)
Ta có \(\left( SAB \right)\cap \left( SCD \right)=Sx//AB//CD\)
Gọi \(I\) là trung điểm của \(AB,\) suy ra \(SI\bot AB\Rightarrow SI\bot Sx\Rightarrow SI\bot \left( SCD \right)\Rightarrow SI\bot SD\)
\(AC=4a\Rightarrow AD=2\sqrt{2}a\Rightarrow DI=a\sqrt{10}\)
Đặt \(SD=x\Rightarrow SI=\sqrt{{{x}^{2}}-2{{a}^{2}}}.\)
Ta có hệ thức \({{x}^{2}}-2{{a}^{2}}+{{x}^{2}}=10{{a}^{2}}\Rightarrow {{x}^{2}}=6{{a}^{2}}\Rightarrow x=a\sqrt{6}\)
Từ đó ta tính được \(SO=a\sqrt{2}.\)
Vậy \({{V}_{ABCD.A'B'C'D'}}=a\sqrt{2}.{{\left( 2\sqrt{2}a \right)}^{2}}=8{{a}^{3}}\sqrt{2}.\)
Chọn đáp án D.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Sở GD&ĐT Hà Tĩnh lần 1 có đáp án
Câu hỏi liên quan
-
Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại \(C,AB=a\sqrt{3},AC=2,SC=a\sqrt{5}.\) Hai mặt phẳng \(\left( SAB \right)\) và \(\left( SAC \right)\) cùng vuông góc với mặt phẳng \(\left( ABC \right).\) Thể tích của khối chóp \(S.ABC\) bằng
-
Hàm số \(y={{x}^{3}}+2\). có bao nhiêu điểm cực trị?
-
Tính thể tích \(V\) của khối lăng trụ tam giác đều có tất cả các cạnh bằng \(a.\)
-
Giá trị nhỏ nhất của hàm số \(y=\frac{3x+1}{x-2}\) trên \(\left[ -1;1 \right]\) bằng
-
Cho khối chóp \(S.ABC\) có \(AB\bot BC,BC\bot SC,SC\bot SA,BC=a,SC=\sqrt{15}a\) và góc giữa \(AB,SC\) bằng \({{30}^{0}}.\) Thể tích khối chóp \(S.ABC\) bằng
-
Cho hàm số có bảng biến thiên như hình vẽ bên. Đặt \(\mathop {\min }\limits_{x \in \left[ { - 2;2} \right]}\,f\left( x \right)=m,\mathop {\max}\limits_{x \in \left[ { - 2;2} \right]}\,f\left( x \right)=M.\) Khẳng định nào dưới đây đúng?
-
Cho hàm số \(y=f\left( x \right)\) có tập xác định \(R\backslash \left\{ -1 \right\},\) có bảng biến thiên như hình vẽ. Đồ thị hàm số có tất cả bao nhiêu tiệm cân đứng và tiệm cận ngang?
.png)
-
Điểm nào sau đây là điểm cực tiểu của đồ thị hàm số \(y={{x}^{3}}-3x+1\)?
-
Đường thẳng \(y=2x+1\) cắt đồ thị hàm số \(y={{x}^{3}}+3{{x}^{2}}+4x-5\) tại
-
Một hình chóp có chiều cao bằng 10cm và diện tích đáy \(30c{{m}^{2}}\) thì có thể tích bằng
-
Cho hàm số \(y=f\left( x \right).\) Hàm số \(y=f'\left( x \right)\) có đồ thị như hình vẽ. Hàm số \(g\left( x \right)=f\left( {{x}^{3}}+1 \right)\) nghịch biến trên khoảng
-
Cho hàm số bậc ba \(y=f\left( x \right)\) có đồ thị trong hình bên. Số nghiệm của phương trình \(f\left( x \right)=1\) là
-
Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình bên. Hàm số đã cho có bao nhiêu điểm cực trị?
-
Cho hàm số \(f\left( x \right)=\left\{ \begin{align} & -{{x}^{2}}+2x\text{ với }x<1 \\ & -2x+3x\text{ với }x\ge 1 \\ \end{align} \right.\). Tìm giá trị nhỏ nhất \(m\) của hàm số trên đoạn \(\left[ -1;2 \right].\)
-
Biết rằng giá trị nhỏ nhất của hàm số \(y=mx+\frac{36}{x+1}\) trên \(\left[ 0;3 \right]\) bằng 20. Mệnh đề nào sau đây đúng?
-
Cho hàm số \(y=f\left( x \right)\) có \(\underset{x\to +\infty }{\mathop{\lim }}\,y=1\) và \(\underset{x\to -\infty }{\mathop{\lim }}\,y=-1.\) Khẳng định nào sau đây là khẳng định đúng?
-
Hàm số \( y=x^4+x^2-2\) nghịch biến trên khoảng nào trong các khoảng sau?
-
Cho hàm số \(y=\frac{x+1}{x-m},\) với \(m\) là tham số thực. Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số đã cho nghịch biến trên khoảng \(\left( 2;+\infty \right)?\)
-
Cho hàm số \(y=-2{{x}^{3}}+6{{x}^{2}}-5\) có đồ thị \(\left( C \right).\) Phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(M\) có hoành độ bằng 3 là
-
Hàm số nào sau đây đồng biến trên khoảng \(\left( { - \infty ;+ \infty} \right)\)
