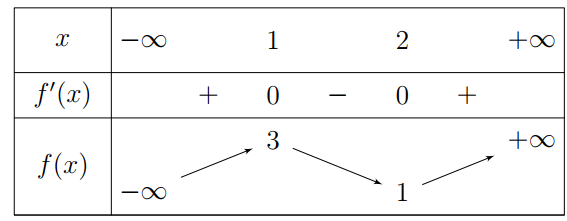
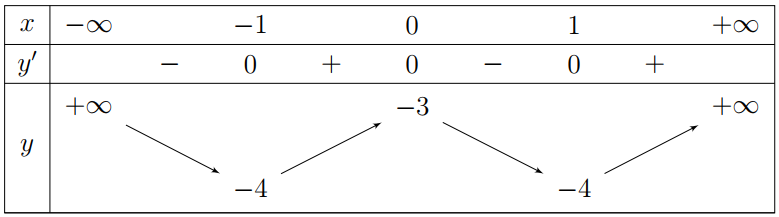
Cho hàm bậc ba \(f\left( x \right)\) có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(g\left( x \right)=\frac{1}{f\left( x \right)-2}\) là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiDựa vào bảng biến thiên, ta thấy phương trình \(2f\left( x \right)-3=0\Leftrightarrow f\left( x \right)=\frac{3}{2}\) có 3 nghiệm \({{x}_{1}};{{x}_{2}};{{x}_{3}}\) và hàm số \(y=f\left( x \right)\) là hàm số bậc ba \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\) có \(a>0.\)
* Ta có \(\underset{x\to x_{1}^{+}}{\mathop{\lim }}\,g\left( x \right)=+\infty \) và \(\underset{x\to x_{1}^{-}}{\mathop{\lim }}\,=-\infty \).
* Ta có \(\underset{x\to x_{2}^{+}}{\mathop{\lim }}\,g\left( x \right)=+\infty \) và \(\underset{x\to x_{2}^{-}}{\mathop{\lim }}\,g\left( x \right)=-\infty \)
* Ta có \(\underset{x\to x_{3}^{+}}{\mathop{\lim }}\,g\left( x \right)=+\infty \) và \(\underset{x\to x_{3}^{-}}{\mathop{\lim }}\,g\left( x \right)=-\infty \)
Suy ra hàm số \(y=g\left( x \right)\) có ba tiệm cận đứng.
Ta có \(\underset{x\to \pm \infty }{\mathop{\lim }}\,g\left( x \right)=0,\) suy ra hàm số \(y=g\left( x \right)\) có TCN là \(y=0.\)
Vậy hàm số có 4 tiệm cận.
Chọn đáp án B.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Sở GD&ĐT Hà Tĩnh lần 1 có đáp án
Câu hỏi liên quan
-
Cho hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\) có đồ thị như hình vẽ. Xét dấu của \(a,b,c.\)
-
Cho khối chóp \(S.ABC\) có \(AB\bot BC,BC\bot SC,SC\bot SA,BC=a,SC=\sqrt{15}a\) và góc giữa \(AB,SC\) bằng \({{30}^{0}}.\) Thể tích khối chóp \(S.ABC\) bằng
-
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau. Mệnh đề nào sau đây SAI?
-
Cho hàm số bậc ba \(y=f\left( x \right)\) có đồ thị trong hình bên. Số nghiệm của phương trình \(f\left( x \right)=1\) là
-
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(R,\) có bảng biến thiên như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho hàm số
\(g\left( x \right)=\left| f\left( \left| 6x-5 \right| \right)+2021+m \right|\)
Có 3 điểm cực đại?
-
Cho hàm số \(f\left( x \right)=\left\{ \begin{align} & -{{x}^{2}}+2x\text{ với }x<1 \\ & -2x+3x\text{ với }x\ge 1 \\ \end{align} \right.\). Tìm giá trị nhỏ nhất \(m\) của hàm số trên đoạn \(\left[ -1;2 \right].\)
-
Cho hàm số \(y=\frac{2x+1}{x-1}.\) Điểm nào sau đây thuộc đồ thị hàm số?
-
Cho lăng trụ tứ giác đều \(ABCD.A'B'C'D'\) có \(AC=4a.\) Gọi \(O\) là tâm của mặt \(A'B'C'D'.\) Biết rằng hai mặt phẳng \(\left( OAB \right)\) và \(\left( OCD \right)\) vuông góc với nhau. Thể tích khối lăng trụ \(ABCD.A'B'C'D'\) bằng
-
Biết rằng giá trị nhỏ nhất của hàm số \(y=mx+\frac{36}{x+1}\) trên \(\left[ 0;3 \right]\) bằng 20. Mệnh đề nào sau đây đúng?
-
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu của hàm số \(y = f'\left( x \right)\) như hình dưới đây.
Số điểm cực trị của hàm số bằng
-
Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
-
Một hình chóp có chiều cao bằng 10cm và diện tích đáy \(30c{{m}^{2}}\) thì có thể tích bằng
-
Điểm nào sau đây là điểm cực tiểu của đồ thị hàm số \(y={{x}^{3}}-3x+1\)?
-
Cho hàm số \(y=-2{{x}^{3}}+6{{x}^{2}}-5\) có đồ thị \(\left( C \right).\) Phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(M\) có hoành độ bằng 3 là
-
Đồ thị hàm số \(y=\frac{{{x}^{2}}-5x+4}{x-2}\) cắt trục hoành tại bao nhiêu điểm?
-
Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm 34 học sinh?
-
Hình đa diện bên có tất cả bao nhiêu mặt?
-
Cho khối chóp \(S.ABCD\) có đáy \(ABCD\). là hình vuông cạnh bằng \(a,\) cạnh bên \(SA\). vuông góc với mặt đáy và \(SA=3a.\) Thể tích của khối chóp \(S.ABCD\) bằng
-
Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(A\) và mặt bên \(ABB'A'\) là hình vuông cạnh bằng \(a\) (tham khảo hình vẽ bên). Tính tang của góc giữa đường thẳng \(BC'\) và mặt phẳng \(\left( ABB'A' \right).\)
-
Cho khối chóp \(S.ABC\) có đáy là tam giác đều cạnh bằng \(2a,\) mặt bên \(SAB\) vuông góc với mặt đáy. Tính khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( SAB \right).\)
