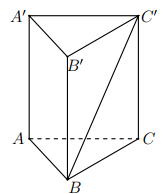
Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(A\) và mặt bên \(ABB'A'\) là hình vuông cạnh bằng \(a\) (tham khảo hình vẽ bên). Tính tang của góc giữa đường thẳng \(BC'\) và mặt phẳng \(\left( ABB'A' \right).\)
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
\(\Delta ABC\) vuông cân tại A nên \(\Rightarrow AB=AC=a.\)
\(\Delta ABA'\) vuông tại \(A\) nên \(\Rightarrow A'B=a\sqrt{2}.\)
Ta có \(\left\{ \begin{align}
& C'A'\bot A'B' \\
& C'A'\bot AA' \\
\end{align} \right.\Rightarrow C'A'\bot \left( ABB'A' \right).\)
\(\Rightarrow BA'\) là hình chiếu của \(BC'\) lên mặt phẳng \(\left( ABB'A' \right).\)
\(\Rightarrow \left( BC',\left( ABB'A' \right) \right)=\left( BC',BA' \right)\)
\(\Delta A'BC'\) vuông tại \(A'\Rightarrow \tan \widehat{A'BC'}=\frac{A'C'}{A'B}=\frac{a}{a\sqrt{2}}=\frac{\sqrt{2}}{2}.\)
Chọn đáp án A.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Sở GD&ĐT Hà Tĩnh lần 1 có đáp án
Câu hỏi liên quan
-
Cho hàm số \(y={{x}^{3}}-m{{x}^{2}}+2x+1\) với \(m\) là tham số thực. Có bao nhiêu giá trị nguyên của \(m\) để hàm số đồng biến trên tập số thực \(R\)?
-
Cho khối chóp \(S.ABC\) có đáy là tam giác đều cạnh bằng \(2a,\) mặt bên \(SAB\) vuông góc với mặt đáy. Tính khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( SAB \right).\)
-
Cho khối chóp \(S.ABC\). Gọi \(M,N\) lần lượt là trung điểm \(SA\) và \(SB.\) Tính tỉ số thể tích của hai khối chóp \(S.MNC\) và \(S.ABC\).
-
Cho lăng trụ tứ giác đều \(ABCD.A'B'C'D'\) có \(AC=4a.\) Gọi \(O\) là tâm của mặt \(A'B'C'D'.\) Biết rằng hai mặt phẳng \(\left( OAB \right)\) và \(\left( OCD \right)\) vuông góc với nhau. Thể tích khối lăng trụ \(ABCD.A'B'C'D'\) bằng
-
Cho hàm số \(y=f\left( x \right).\) Hàm số \(y=f'\left( x \right)\) có đồ thị như hình vẽ. Hàm số \(g\left( x \right)=f\left( {{x}^{3}}+1 \right)\) nghịch biến trên khoảng
-
Cho khối chóp \(S.ABC\) có \(AB\bot BC,BC\bot SC,SC\bot SA,BC=a,SC=\sqrt{15}a\) và góc giữa \(AB,SC\) bằng \({{30}^{0}}.\) Thể tích khối chóp \(S.ABC\) bằng
-
Một chất điểm chuyển động theo quy luật \(s\left( t \right)={{t}^{2}}-\frac{1}{6}{{t}^{3}}\left( m \right).\) Tìm thời điểm \(t\) (giây) mà tạo đó vận tốc \(v\left( m/s \right)\) của chuyển động đạt giá trị lớn nhất.
-
Cho hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\) có đồ thị như hình vẽ. Xét dấu của \(a,b,c.\)
-
Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình bên. Hàm số đã cho có bao nhiêu điểm cực trị?
-
Tiệm cận đứng của đồ thị hàm số \(y=\frac{x+1}{x+3}\) bằng
-
Người ta muốn xây một bể chứa nước dạng hình hộp chữ nhật không nắp có thể tích bằng \(200{{m}^{3}}\) đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công cây bể là 300.000 đồng/\({{m}^{2}}\). Chi phí xây dựng thấp nhất là
-
Biết rằng giá trị nhỏ nhất của hàm số \(y=mx+\frac{36}{x+1}\) trên \(\left[ 0;3 \right]\) bằng 20. Mệnh đề nào sau đây đúng?
-
Cho hàm số \(y=f\left( x \right)\) có tập xác định \(R\backslash \left\{ -1 \right\},\) có bảng biến thiên như hình vẽ. Đồ thị hàm số có tất cả bao nhiêu tiệm cân đứng và tiệm cận ngang?
.png)
-
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( \sqrt[3]{f\left( x \right)+m} \right)={{x}^{3}}-m\) có nghiệm \(x\in \left[ 1;2 \right]\) biết \(f\left( x \right)={{x}^{5}}+3{{x}^{3}}-4m.\)
-
Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
-
Diện tích ba mặt của hình hộp chữ nhật lần lượt là \(15c{{m}^{2}},24c{{m}^{2}},40c{{m}^{2}}.\) Thể tích của khối hộp đó là
-
Thể tích của khối lăng trụ có chiều cao bằng \(h\) và diện tích đáy bằng \(B\) là
-
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu của hàm số \(y = f'\left( x \right)\) như hình dưới đây.
Số điểm cực trị của hàm số bằng
-
Hình đa diện bên có tất cả bao nhiêu mặt?
-
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên. Hàm số nghịch biến trên khoảng nào dưới đây?
