Cho hình chóp S.ABCD có đáy là hình vuông cạnh \(2\sqrt{2}\). Canh bên SA vuông góc với mặt phẳng đáy và SA=3 . Mặt phẳng \((\alpha)\) qua A và vuông góc vói SC cắt canh SB, SC, SD lần lươt tai M, N, P . Thể tích V của khối cầu ngoại tiếp tứ diện CMNP.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai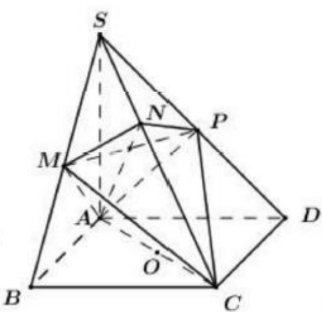
Ta có
\(\begin{array}{l} \left\{\begin{array}{l} B C \perp A B \\ B C \perp S A \end{array} \Rightarrow B C \perp(S A B) \Rightarrow B C \perp A M\right. \\ \left\{\begin{array}{l} A M \perp B C \\ A M \perp S C \end{array} \Rightarrow A M \perp(S B C) \Rightarrow A M \perp M C\right. \end{array}\)
\(\Rightarrow \widehat{ A M C}=90^{\circ}\) hay điểm M thuộc mặt cầu đường kính AC.
Tương tự ta có \(A P \perp(S C D) \Rightarrow A P \perp P C \Rightarrow \widehat{ A P C}=90^{\circ}\)
hay P thuộc măt cầu đường kính AC.
lại có \(A N \perp S C \Rightarrow \widehat {A N C}=90^{\circ}\)hay N thuộc mặt cầu đường kính AC.
Do đó CMNP nội tiếp khối cầu đường kính AC hay khối cầu ngoại tiếp tứ diện CMNP có bán kính \(R=\frac{1}{2} A C=\frac{1}{2} \cdot 2 \sqrt{2} \cdot \sqrt{2}=2\)
Thể tích cần tìm là \(V=\frac{4}{3} \pi R^{3}=\frac{4}{3} \pi \cdot 2^{3}=\frac{32 \pi}{3}\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT chuyên Thái Bình