Cho hình chóp S.ABC có đáy ABC là tam giác vuông tai A, \(\widehat{ A B C}=30^{\circ}\). Tam giác SAB đều cạnh a và hình chiếu vuông góc cùa S lên mặt phẳng (A B C) là trung điểm của cạnh A B . Thề tích của khối chóp S .ABC là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai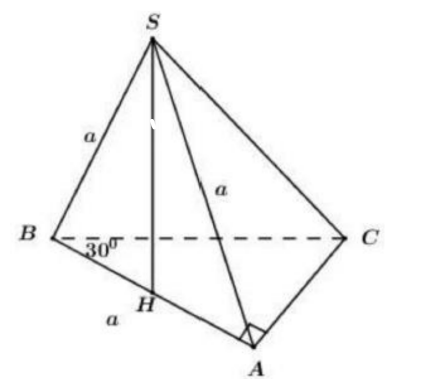
Gọi H là trung điểm AB\(A B \Rightarrow S H \perp(A B C)\)
Tam giác SAB đều cạnh a\(a \Rightarrow S H=\frac{a \sqrt{3}}{2}\)
Xét tam giác vuông ABC:
\(A C=A B \cdot \tan 30^{\circ}=\frac{a \sqrt{3}}{3} \Rightarrow S_{\mathrm{ABC}}=\frac{1}{2} A B \cdot A C=\frac{1}{2} \cdot a \cdot \frac{a \sqrt{3}}{3}=\frac{a^{2} \sqrt{3}}{6}\)\(\Rightarrow V_{S, A B C}=\frac{1}{3} S H S_{\Delta A B C}=\frac{1}{3} \cdot \frac{a \sqrt{3}}{2} \cdot \frac{a^{2} \sqrt{3}}{6}=\frac{a^{3}}{12}\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT chuyên Thái Bình