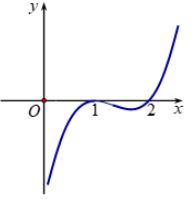
Cho hàm số \(y = f\left( x \right).\) liên tục trên R. Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số \(y = f\left( {{x^2}} \right)\) đồng biến trên khoảng nào dưới đây?
.JPG)
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(y = f\left( {{x^2}} \right) \Rightarrow y' = 2x.f'\left( {{x^2}} \right)\)
Xác định khoảng đồng biến của hàm số, ta có 2 trường hợp:
TH1: \(\left\{ \begin{array}{l}x > 0\\f'\left( {{x^2}} \right) > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\\left[ \begin{array}{l}{x^2} < - 1\\1 < {x^2} < 4\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\\left[ \begin{array}{l} - 2 < x < - 1\\1 < x < 2\end{array} \right.\end{array} \right. \Leftrightarrow 1 < x < 2\)
TH2: \(\left\{ \begin{array}{l}x < 0\\f'\left( {{x^2}} \right) < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 0\\\left[ \begin{array}{l} - 1 < {x^2} < 1\\{x^2} > 4\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 0\\\left[ \begin{array}{l} - 1 < x < 1\\x > 2\\x < - 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x < - 2\\ - 1 < x < 0\end{array} \right.\)
Vậy, hàm số \(y = f\left( {{x^2}} \right)\) đồng biến trên các khoảng \(\left( { - \infty ; - 2} \right),\,\,\left( { - 1;0} \right),\,\,\left( {1;2} \right)\).
Chọn: B
Câu hỏi liên quan
-
Tính thể tích \(V\) của khối lăng trụ tam giác đều có tất cả các cạnh bằng \(a\).
-
Đồ thị sau đây là của hàm số\(y = {x^4} - 3{x^2} - 3\). Với giá trị nào của m thì phương trình \({x^4} - 3{x^2} + m = 0\)có ba nghiệm phân biệt ?
.JPG)
-
Cho hàm số \(y = f(x)\)có đạo hàm liên tục trên \(\mathbb{R},\) hàm số \(y = f'(x - 2)\) có đồ thị như hình bên. Số điểm cực trị của hàm số \(y = f(x)\) là
.JPG)
-
Giá trị nhỏ nhất của hàm số \(y = \dfrac{{2x + 1}}{{1 - x}}\) trên đoạn [ 2 ; 3 ] bằng:
-
Cho hàm số \(f\left( x \right)\) xác định trên \(R\backslash {\rm{\{ 0\} }}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
.JPG)
Hàm số đã cho có bao nhiêu điểm cực trị ?
-
Tính đạo hàm của hàm số \(f\left( x \right) = x\left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 2018} \right)\) tại điểm \(x = 0\).
-
Cho hàm số \(y = f(x)\)có đồ thị như hình vẽ dưới đây. Hàm số \(y = f(x)\)có bao nhiêu điểm cực tiểu?
.JPG)
-
Cho tam giác ABC vuông cân tại A có BC =2. Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {CA} \):
-
Cho hình chữ nhật \(MNPQ.\) Phép tịnh tiến theo véc tơ \(\overrightarrow {MN} \) biến điểm \(Q\) thành điểm nào?
-
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(SA \bot \left( {ABCD} \right).\) Khẳng định nào dưới đây sai?
-
Cho hình vuông \(ABCD\) tâm \(O\) cạnh \(a\). Biết rằng tập hợp các điểm \(M\) thỏa mãn \(2M{A^2} + M{B^2} + 2M{C^2} + M{D^2} = 9{a^2}\) là một đường tròn. Bán kính của đường tròn đó là:
-
Tính số chỉnh hợp chập \(5\) của \(8\) phần tử.
-
Tìm số tự nhiên \(n\) thỏa mãn \(\dfrac{{C_n^0}}{{1.2}} + \dfrac{{C_n^1}}{{2.3}} + \dfrac{{C_n^2}}{{3.4}} + ... + \dfrac{{C_n^n}}{{\left( {n + 1} \right)\left( {n + 2} \right)}} = \dfrac{{{2^{2018}} - n - 3}}{{\left( {n + 1} \right)\left( {n + 2} \right)}}\).
-
Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \dfrac{{2018}}{{\sin x}}.\)
-
Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; AB = AD = 2a;CD = a . Góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 600 . Gọi I là trung điểm của AD. Biết 2 mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD.
-
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(SA\) vuông góc với đáy, mặt bên \(\left( {SCD} \right)\) hợp với đáy một góc bằng \(60^\circ \), \(M\) là trung điểm của \(BC\). Biết thể tích khối chóp \(S.ABCD\) bằng \(\dfrac{{{a^3}\sqrt 3 }}{3}\). Khoảng cách từ \(M\) đến mặt phẳng \(\left( {SCD} \right)\) bằng:
-
Có 5 học sinh lớp 12A1, 3 học sinh lớp 12A2, 2 học sinh lớp 12D1. Xếp ngẫu nhiên 10 học sinh trên thành một hàng dài. Tính xác suất để trong 10 học sinh trên không có hai học sinh cùng lớp đứng cạnh nhau.
-
Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a. Các cạnh bên SA, SB, SC tạo với đáy một góc 60o. Gọi D là giao điểm của SA với mặt phẳng qua BC và vuông góc với SA. Tính theo a thể tích khối chóp S.DBC
-
Tính \(\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {4{x^2} + 8x + 1} + 2x} \right)\) bằng
-
Đồ thị sau đây là của hàm số nào?
.JPG)
