Đề thi giữa HK2 lớp 10 môn Toán năm 2022-2023
Trường THPT Lê Quý Đôn
-
Câu 1:
Cho hàm số y=f(x)=ax2+bx+cy=f(x)=ax2+bx+c có đồ thị như hình bên. Dấu của hệ số aa và biệt thức Δ Δ là
.png)
A. a>0, Δ >0a>0, Δ >0.
B. a<0,Δ>0a<0,Δ>0.
C. a<0,Δ>0a<0,Δ>0.
D. a<0, Δ =0a<0, Δ =0.
-
Câu 2:
Bất phương trình nào sau đây có tập nghiệm là S=R∖{2}S=R∖{2} ?
A. x2+4x+5≤0x2+4x+5≤0.
B. −2x2+5x−11>0−2x2+5x−11>0.
C. −3x2+12x−12<0−3x2+12x−12<0.
D. −3x2+12x−12≥0−3x2+12x−12≥0.
-
Câu 3:
Giá trị của tham số mm để phương trình x2−(m+1)x+4=0x2−(m+1)x+4=0 có nghiệm là
A. (−5;3)(−5;3).
B. (−∞;−5]∪[3;+∞)(−∞;−5]∪[3;+∞).
C. [−5;3][−5;3].
D. (−∞;−5)∪(3;+∞)(−∞;−5)∪(3;+∞).
-
Câu 4:
Cho tam thức bậc hai f(x)=mx2+2x+mf(x)=mx2+2x+m. Giá trị của tham số mm để f(x)≥0,∀x∈Rf(x)≥0,∀x∈R là
A. m≥1m≥1.
B. m>1m>1.
C. m>0m>0.
D. m<2m<2.
-
Câu 5:
Cho bất phương trình −x2−2mx+m2−2m≤0−x2−2mx+m2−2m≤0. Giá trị của mm để bất phương trình có nghiệm đúng với mọi x∈Rx∈R là
A. 0≤m≤10≤m≤1.
B. 0<m<10<m<1.
C. 1≤m≤21≤m≤2.
D. 1<m<21<m<2.
-
Câu 6:
Tập nghiệm của bất phương trình 2x2−3x+4x2+2>12x2−3x+4x2+2>1 là
A. (−∞;−1)∪(2;+∞)(−∞;−1)∪(2;+∞).
B. (−∞;−2)∪(−1;+∞)(−∞;−2)∪(−1;+∞).
C. (−∞;1)∪(2;+∞)(−∞;1)∪(2;+∞).
D. (−∞;2)∪(4;+∞)(−∞;2)∪(4;+∞).
-
Câu 7:
Tam thức bậc hai f(x)=−x2+5x−6.f(x)>0f(x)=−x2+5x−6.f(x)>0 khi và chỉ khi
A. x∈(−∞;2)x∈(−∞;2).
B. (3;+∞)(3;+∞).
C. x∈(2;+∞)x∈(2;+∞).
D. x∈(2;3)x∈(2;3).
-
Câu 8:
Số giá trị nguyên của xx để 2x2−7x−9<02x2−7x−9<0 là
A. 3.
B. 4.
C. 5.
D. 6.
-
Câu 9:
Bảng xét dấu nào sau đây là của tam thức f(x)=−x2+4x−4f(x)=−x2+4x−4 ?
A.

B.
.png)
C.
.png)
D.
.png)
-
Câu 10:
Tìm tập nghiệm của hệ bất phương trình {x2−4x+3>0x2−6x+8>0.
A. (−∞;1)∪(3;+∞).
B. (−∞;1)∪(4;+∞).
C. (−∞;2)∪(3;+∞).
D. (1;4).
-
Câu 11:
Cho bất phương trình x2+4x+|x+2|−m≤0. Xác định m để bất phương trình có nghiệm.
A. −174≤m≤−4.
B. m≤−4.
C. m≥−174.
D. m≥−4.
-
Câu 12:
Cho phương trình (m−5)x2+2(m−1)x+m=0 (1). Với giá trị nào của m thì (1) có 2 nghiệm x1,x2 thỏa x1<1<x2 ?
A. m≥5.
B. m<74.
C. 74<m<5.
D. 74≤m≤5.
-
Câu 13:
Điều kiện xác định của phương trình √x−1+√x−2=√x−3 là:
A. (3;+∞).
B. [2;+∞).
C. [1;+∞).
D. [3;+∞).
-
Câu 14:
Phương trình sau có bao nhiêu nghiệm √x=√−x ?
A. 0.
B. 1.
C. 2.
D. Vô số.
-
Câu 15:
Tập nghiệm của phương trình x−√x−3=√3−x+3 là:
A. S=∅.
B. S={3}.
C. S=[3;+∞).
D. S=R.
-
Câu 16:
Phương trình √f(x)=√g(x) tương đương với phương trình nào sau đây?
A. f(x)=g(x).
B. f2(x)=g2(x).
C. [f(x)≥0f(x)=g(x).
D. {f(x)≥0f(x)=g(x)
-
Câu 17:
Phương trình (x−4)2=x−2 là phương trình hệ quả của phương trình nào sau đây?
A. x−4=x−2.
B. √x−2=x−4.
C. √x−4=√x−2.
D. √x−4=x−2.
-
Câu 18:
Số giá trị nguyên của m để phương trình √x2−x+m=√x−3 có hai nghiệm phân biệt là
A. 0.
B. 1.
C. 2.
D. 3.
-
Câu 19:
Trong mặt phẳng toạ độ Oxy, cho →a=(−4;2),→b=(2k;−k). Với giá trị nào của k dưới đây thì →a=→b?
A. k=−12.
B. k=2.
C. k=−2.
D. Không tồn tại k.
-
Câu 20:
Trong mặt phẳng toạ độ Oxy, cho →a=(−m+2n;−1),→b=(5;−m−n). Với giá trị nào của m,n dưới đây thì →a=→b ?
A. m=−1,n=2.
B. m=2,n=−1.
C. m=2,n=1.
D. Không tồn tại m,n.
-
Câu 21:
Trong mặt phẳng toạ độ Oxy, cho A(2;−3),B(−4;1) và C(−1;−1). Khẳng định nào dưới đây là đúng?
A. →AB=2→AC.
B. →AB=12→AC.
C. →AB=−2→AC
D. →AB=−12→AC.
-
Câu 22:
Trong mặt phẳng toạ độ Oxy, cho đường thẳng d:{x=−2−ty=4+3t.Trong các vectơ sau, vectơ nào là vectơ chỉ phương của d ?
A. →u=(−2;4).
B. →v=(3;1).
C. →m=(−1;−3).
D. →n=(−1;3).
-
Câu 23:
Trong mặt phẳng toạ độ Oxy, cho đường thẳng Δ :x−3y−2=0. Trong các vectơ sau, vectơ nào là vectơ pháp tuyến của Δ ?
A. →u=(−3;1).
B. →v=(3;1).
C. →m=(−1;−3).
D. →n=(1;−3).
-
Câu 24:
Trong mặt phẳng toạ độ Oxy, cho đường thẳng Δ :−x+2y−2=0. Trong các vectơ sau, vectơ nào là vectơ chỉ phương của Δ ?
A. →u=(−1;2).
B. →v=(−2;−1).
C. →m=(−2;1).
D. →n=(1;2).
-
Câu 25:
Trong mặt phẳng toạ độ Oxy, cho đường thẳng d:{x=−2ty=4+t. Trong các vectơ sau, vectơ nào là vectơ pháp tuyến của d ?
A. →u=(−2;1).
B. →v=(2;−1).
C. →m=(1;−2).
D. →n=(1;2).
-
Câu 26:
Đường thẳng đi qua A(−3;2) và nhận →n=(1;5) làm vectơ pháp tuyến có phương trình tổng quát là:
A. x+5y+7=0.
B. −x+5y−13=0.
C. −5x+y−17=0.
D. x+5y−7=0.
-
Câu 27:
Phương trình tham số của đường thẳng d đi qua A(0;−2) và có vectơ chỉ phương →u=(2;−3) là:
A. {x=2ty=−2−3t
B. {x=2y=−3−2t
C. {x=3ty=3+2t
D. {x=2+ty=−3−2t
-
Câu 28:
Phương trình tham số của đường thẳng d:x4−y3=1 là:
A. {x=4+3ty=4t
B. {x=4−4ty=3t
C. {x=4+4ty=3t
D. {x=4−3ty=4t
-
Câu 29:
Góc giữa hai đường thẳng Δ 1:−2x+y−7=0 và Δ 2:{x=2−ty=1+3t. là
A. 30∘.
B. 45∘.
C. 60∘.
D. 90∘.
-
Câu 30:
Trong mặt phẳng toạ độ, cho ba điểm A,B,C và đường thẳng Δ đi qua hai điểm A,B (xem hình bên). Khoảng cách từ C đến đường thẳng Δ là bao nhiêu?
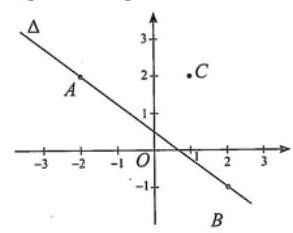
A. 59.
B. 95.
C. 85.
D. 45.
-
Câu 31:
Cho đường thẳng d:3x−2y+1=0 và điểm M(1;2). Phương trình đường thẳng Δ qua M và tạo với d một góc 45∘ là
A. 2x−y=0 và 5x+y−7=0.
B. x−5y+9=0 và 3x+y−5=0.
C. 3x−2y+1=0 và 5x+y−7=0.
D. x−5y+9=0 và 5x+y−7=0.
-
Câu 32:
Khoảng cách từ O(0;0) đến đường thẳng Δ :4x−3y−5=0 là
A. −5.
B. 0.
C. 1.
D. 15.
-
Câu 33:
Trong mặt phẳng toạ độ, đường tròn tâm I(3;−1) và bán kính R=2 có phương trình là
A. (x+3)2+(y−1)2=4.
B. (x−3)2+(y−1)2=4.
C. (x−3)2+(y+1)2=4.
D. (x+3)2+(y+1)2=4.
-
Câu 34:
Phương trình đường tròn tâm I(3;−2) và đi qua điểm M(−1;1) là
A. (x+3)2+(y−2)2=5.
B. (x−3)2+(y+2)2=25.
C. (x−3)2+(y+2)2=5.
D. (x−3)2+(y−2)2=25.
-
Câu 35:
Phương trình đường tròn có đường kính AB với A(−1;2) và B(3;2) là
A. (x+1)2+(y+2)2=4.
B. (x+1)2+(y−2)2=16.
C. (x−1)2+(y−2)2=4.
D. (x−3)2+(y−2)2=16.














